
【题目】如图,已知钝角△ABC
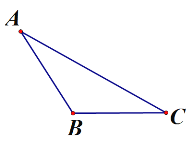
(1)过点A作BC边的垂线,交CB的延长线于点D;(尺规作图,保留作图痕迹,不要求写作法)
(2)当BC=AB,∠ABC=120°时,求证:AB平分∠DAC。
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】为了美化环境,建设最美西安,我市准备在一个广场上种植甲、乙两种花卉,经市场调查,甲种花卉的种植费用为y(元)与种植面积x(m2)之间的函数关系如图所示,乙种花卉的种植费用为100元/m2.
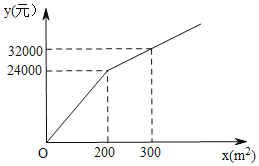
(1)求y与x之间的函数关系式;
(2)广场上甲、乙两种花卉的种植面积共1200m2,若甲种花卉的种植面积不少于200m2,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少费用为多少元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学计划购买A型和B型课桌凳共200套,经招标,购买一套A型课桌凳比购买一套B型课桌凳少用40元,,且购买4套A型和6套B型课桌凳共需1820元。
(1)求购买一套A型课桌凳和一套B型课桌凳各需多少元?
(2)学校根据实际情况,要求购买这两种课桌凳总费用不能超过40880元,并且购买A型课桌凳的数量不能超过B型课桌凳的![]() ,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
查看答案和解析>>
科目:初中数学 来源: 题型:
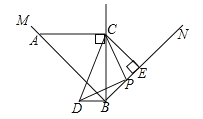
【题目】如图,∠MBN=90°,点C是∠MBN平分线上的一点,过点C分别作AC⊥BC,CE⊥BN,垂足分别为点C,E,AC=![]() ,点P为线段BE上的一点(点P不与点B、E重合),连接CP,以CP为直角边,点P为直角顶点,作等腰直角三角形CPD,点D落在BC左侧.
,点P为线段BE上的一点(点P不与点B、E重合),连接CP,以CP为直角边,点P为直角顶点,作等腰直角三角形CPD,点D落在BC左侧.
(1)求证:![]() ;
;
(2)连接BD,请你判断AC与BD的位置关系,并说明理由;
(3)设PE=x,△PBD的面积为S,求S与x之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与反比例函数
与反比例函数![]() 在第一象限内的图象相交于点
在第一象限内的图象相交于点![]() .
.
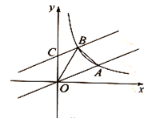
(1)求反比例函数的解析式;
(2)将直线![]() 向上平移后与反比例函数图象在第一象限内交于点
向上平移后与反比例函数图象在第一象限内交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且
,且![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
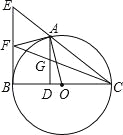
【题目】如图,A是以BC为直径的⊙O上的一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,点F是EB的中点,连结CF交AD于点G
(1)求证:AF是⊙O的切线;
(2)求证:AG=GD;
(3)若FB=FG,且⊙O的半径长为3![]() ,求BD.
,求BD.
查看答案和解析>>
科目:初中数学 来源: 题型:
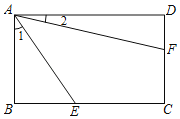
【题目】如图,矩形ABCD长与宽的比为5:3,点E、F分别在边BC、CD上,tan∠1=![]() ,tan∠2=
,tan∠2=![]() ,则cos(∠1+∠2)的值为( )
,则cos(∠1+∠2)的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.

(1)求证:AD=AF;
(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为3的正三角形ABC放置在直线l上(AB与直线l重合),将正三角形ABC沿直线l向右做无滑动的滚动,正三角形ABC的任意一边与直线l重合时记录滚动次数,例如,正三角形ABC由图中位置①滚动到位置②时记录为滚动一次,当正三角形ABC由图中位置①开始滚动2018次时,点A经过的路径总长度为( )

A.2690πB.2692πC.4034πD.4036π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com