
 如图,E、F分别是矩形ABCD边AD、BC上的点,连接AF、CE,恰有∠BFA=∠DEC,则AF与CE的位置关系是( )
如图,E、F分别是矩形ABCD边AD、BC上的点,连接AF、CE,恰有∠BFA=∠DEC,则AF与CE的位置关系是( )| A. | 互相平行 | B. | 互相垂直 | C. | 不相交也不平行 | D. | 无法确定 |
分析 根据等角的补角相等可得∠AEC=∠CFA,再根据矩形的性质可得∠D=∠B=90°=∠BAD=∠DCB=90°,进而可得∠BAF=∠DCE,然后可证明∠EAF=∠ECF,根据两组对角分别相等的四边形是平行四边形可得四边形AECF是平行四边形,再根据平行四边形的性质可得AF∥CE.
解答 解:∵∠BFA=∠DEC,
∴∠AEC=∠CFA,
∵四边形ABCD是矩形,
∴∠D=∠B=90°,∠BAD=∠DCB=90°,
∴∠AFB+∠FAB=∠DEC+∠ECD=90°,
∴∠BAF=∠DCE,
∴∠EAF=∠ECF,
∴四边形AECF是平行四边形,
∴AF∥CE,
故选:A.
点评 此题主要考查了平行线的判定,以及平行四边形的判定和性质,关键是掌握等角的补角相等,等角的余角相等.


科目:初中数学 来源: 题型:填空题
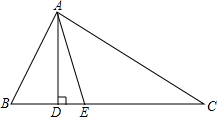 如图,△ABC中,AD⊥BC于D,AE平分∠BAC交BC边于点E,∠C=2∠DAE,AC=11,AB=6,则CE=$\frac{55}{6}$.
如图,△ABC中,AD⊥BC于D,AE平分∠BAC交BC边于点E,∠C=2∠DAE,AC=11,AB=6,则CE=$\frac{55}{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 为了了解一批汽车轮胎的使用年限,应采用抽样调查的方式 | |
| B. | “50名同学中恰有2名同学的生日是同一天”属于随机事件 | |
| C. | “早晨的太阳从东方升起”属于必然事件 | |
| D. | “长为3cm,5cm,9cm的三条线段围成一个三角形”属于可能事件 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 购买数量(贴) | 单价(元/贴) |
| 不超过10贴(包含10贴) | 9 |
| 超过10贴不超过m贴的部分(15≤m≤30) | 8 |
| 超过m贴的部分 | 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
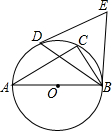 如图,△ABC内接于⊙O,∠A=30°,AB是⊙O的直径,D是劣弧AC的中点,连接BD,分别过点B、D作⊙O的切线,两条切线相交于点E,则△BDE的形状是( )
如图,△ABC内接于⊙O,∠A=30°,AB是⊙O的直径,D是劣弧AC的中点,连接BD,分别过点B、D作⊙O的切线,两条切线相交于点E,则△BDE的形状是( )| A. | 直角三角形 | B. | 等腰直角三角形 | C. | 等边三角形 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
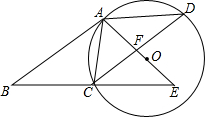 如图,在?ABCD中,AC=AD,⊙O是△ACD的外接圆,BC的延长线与AO的延长线交干E.
如图,在?ABCD中,AC=AD,⊙O是△ACD的外接圆,BC的延长线与AO的延长线交干E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
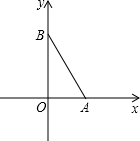 如图,△OAB中,∠AOB=90°,AO=1,BO=2.以AO为x轴,BO为y轴建立平面直角坐标系,O为原点.二次函数y=x2+bx+c的图象经过点A,B.
如图,△OAB中,∠AOB=90°,AO=1,BO=2.以AO为x轴,BO为y轴建立平面直角坐标系,O为原点.二次函数y=x2+bx+c的图象经过点A,B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com