
【题目】如图,在平面直角坐标系中,直线AC的表达式为![]() ,直线
,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,有一动点
,有一动点![]() 在线段
在线段![]() 和线段
和线段![]() 上运动.
上运动.
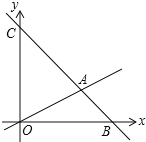
(1)求直线![]() 的表达式.
的表达式.
(2)求![]() 的面积.
的面积.
(3)是否存在点M,使![]() 的面积是
的面积是![]() 的面积的
的面积的![]() ?若存在请直接写出点M的坐标.
?若存在请直接写出点M的坐标.
【答案】(1)y=![]() x;(2)12;(3)M的坐标为(1,
x;(2)12;(3)M的坐标为(1,![]() )或(1,5).
)或(1,5).
【解析】
(1)利用待定系数法求直线OA的解析式;
(2)根据三角形面积公式计算;
(3)根据三角形的面积公式可判断M的横坐标是1,然后把x=1分别代入OA和AC的解析式中计算对应的函数值即可得到M点的坐标.
(1)设直线OA的表达式为y=kx,将点A(4,2)代入得2=4k,解得k=![]() ,
,
所以直线AB的解析式为y=![]() x;
x;
(2)在y=-x+6中,当x=0,y=6,则C(0,6),
S△OAC=![]() ×6×4=12;
×6×4=12;
(3)∵当△OMC的面积是△OAC的面积的![]() 时,
时,
∴M的横坐标是![]() ×4=1,
×4=1,
当点M在线段OA上时,把x=1代入y=![]() x得y=
x得y=![]() ,则此时M(1,
,则此时M(1,![]() );
);
当点M在线段AC上时,把x=1代入y=-x+6得y=5,则此时M(1,5),
综上所述,M的坐标为(1,![]() )或(1,5).
)或(1,5).


科目:初中数学 来源: 题型:
【题目】(观察)
![]() ,
,![]() ,
,![]() ,……,
,……,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,……,
,……,![]() ,
,![]() ,
,![]() .
.
(发现)
根据你的阅读回答问题:
(1)上述内容中,两数相乘,积的最大值为______;
(2)设参与上述运算的第一个因数为![]() ,第二个因数为
,第二个因数为![]() ,用等式表示
,用等式表示![]() 与
与![]() 的数量关系是____.
的数量关系是____.
(类比)
观察下列两数的积:1×49,2×48,3×47,4×46,……m×n,……46×4,47×3,48×2,49×1
猜想![]() 的最大值为_______,并用你学过的知识加以证明.
的最大值为_______,并用你学过的知识加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背景介绍)勾股定理是几何学中的明珠,充满着魅力.千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者.向常春在1994年构造发现了一个新的证法.

(小试牛刀)把两个全等的直角三角形如图1放置,其三边长分别为a、b、c.显然,∠DAB=∠B=90°,AC⊥DE.请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积,再探究这三个图形面积之间的关系,可得到勾股定理:
S梯形ABCD= ,
S△EBC= ,
S四边形AECD= ,
则它们满足的关系式为 ,经化简,可得到勾股定理.
(知识运用)(1)如图2,铁路上A、B两点(看作直线上的两点)相距40千米,C、D为两个村庄(看作两个点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=25千米,BC=16千米,则两个村庄的距离为 千米(直接填空);
(2)在(1)的背景下,若AB=40千米,AD=24千米,BC=16千米,要在AB上建造一个供应站P,使得PC=PD,请用尺规作图在图2中作出P点的位置并求出AP的距离.
(知识迁移)借助上面的思考过程与几何模型,求代数式![]() 最小值(0<x<16)
最小值(0<x<16)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人进行射击选拔赛,各射击10发子弹,成绩如下表:
环数命中 | 5环 | 6环 | 7环 | 8环 | 9环 | 10环 |
甲(次) | 1 | 1 | 1 | 3 | 2 | 2 |
乙(次) | 0 | 2 | 0 | 5 | 2 | 1 |
(1)计算甲、乙的平均成绩.
(2)如果你是甲、乙的教练,你会选择谁去参加正式比赛?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.

(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知△ABC中,AB=BC=1,∠ABC=90°,把一块含30°角的直角三角板DEF的直角顶点D放在AC的中点上(直角三角板的短直角边为DE,长直角边为DF),将直角三角板DEF绕D点按逆时针方向旋转.

(1)在图1中,DE交边AB于M,DF交边BC于N,证明:DM=DN;
(2)在这一旋转过程中,直角三角板DEF与△ABC的重叠部分为四边形DMBN,请说明四边形DMBN的面积是否发生变化?若发生变化,请说明是如何变化的?若不发生变化,求出其面积;
(3)继续旋转至如图2的位置,延长AB交DE于M,延长BC交DF于N,DM=DN是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两直线l1:y=kx﹣2b+1和l2:y=(1﹣k)x+b﹣1交于x轴上一点A,与y轴分别交于点B、C,若A的横坐标为2.
(1)求这两条直线的解析式;
(2)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家的洗手盆上装有一种抬启式水龙头(如图1),完全开启后,把手AM的仰角α=37°,此时把手端点A、出水口B和点落水点C在同一直线上,洗手盆及水龙头的相关数据如图2.(参考数据:sin37°=![]() ,cos37°=
,cos37°=![]() ,tan37°=
,tan37°=![]() )
)
求把手端点A到BD的距离;
求CH的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com