
【题目】如图,直线AB、CD相交于点O,OE是∠COB的平分线,FO⊥OE,已知∠AOD=70°.
(1)求∠BOE的度数; (2)OF平分∠AOC吗?为什么?

科目:初中数学 来源: 题型:
【题目】已知:A(0,1),B(2,0),C(4,3)
(1)在直角坐标系中描出各点,画出△ABC.
(2)求△ABC的面积;
(3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小兵早上从家匀速步行去学校,走到途中发现数学书忘在家里了,随即打电话给爸爸,爸爸立即送书去,小兵掉头以原速往回走,几分钟后,路过一家书店,此时还未遇到爸爸,小兵便在书店挑选了几支笔,刚付完款,爸爸正好赶到,将书交给了小兵.然后,小兵以原速继续上学,爸爸也以原速返回家.爸爸到家后,过一会小兵才到达学校.两人之间的距离y(米)与小兵从家出发的时间x(分钟)的函数关系如图所示.则家与学校相距米.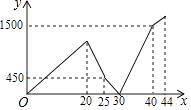
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB的边OB上的一点.

(1)过点P画OB的垂线,交OA于点C;
(2)过点P画OA的垂线,垂足为点H;
(3)线段PH的长度是点P到直线________的距离,线段_________的长度是点C到直线OB的距离,PC、PH、OC这三条线段的大小关系是__________(用“<”号连接).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=60°,M为对角线BD延长线上一点,连接AM和CM,E为CM上一点,且满足CB=CE,连接BE,交CD于点F.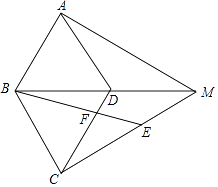
(1)若∠AMB=30°,且DM=3,求BE的长;
(2)证明:AM=CF+DM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行学生“爱校·爱家·爱国”主题演讲比赛,某同学将选手们的得分进行统计,绘制成如图所示的得分条形图下列四个判断:

①共有10人得6分;
②得5分和7分的人数一样多;
③8名选手的成绩高于8分;
④共有25名选手参赛.
其中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com