
分析 正三角形ABC中,可通过全等三角形来证明BM=CN,由于∠BON=∠MBC+∠BCO=60°,而∠ACB=∠ACN+∠OCB=60°,因此∠ACN=∠MBC,又知道∠A=∠BCM=60°,AC=BC,因此△ACN≌△CBM,可得出BM=CN;
正方形和正五边形的证明过程与正三角形的一样,都是通过全等三角形来得出线段的相等,证三角形的过程中都是根据∠BON和多边形的内角相等得出一组两三角形中的一组对应角相等,然后根据正多边形的内角和边相等,得出△BCM和△CND全等,进而得出BM=CN.
解答 证明:在图一中,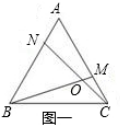
∵△ABC是正三角形,
∴BC=CA,∠BCM=∠CAN=60°,
∵∠BON=60°,
∴∠CBM+∠BCN=60°.
∵∠BCN+∠ACN=60°,
∴∠CBM=∠ACN.
∴△BCM≌△CAN(ASA).
∴BM=CN.
(1)如图二,在正方形ABCD中,M、N分别是CD、AD上的点,BM与CN相交于点O,若∠BON=90°,则BM=CN.
证明:在图二中,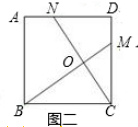
∵四边形ABCD是正方形,
∴BC=CD,∠BCM=∠CDN=90°.
∵∠BON=90°,
∴∠CBM+∠BCN=90°.
∵∠BCN+∠DCN=90°,
∴∠CBM=∠DCN.
∴△BCM≌△CDN(ASA).
∴BM=CN.
(2)如图三,在正五边形ABCDE中,M、N分别是CD、DE上的点,BM与CN相交于点,若∠BON=108°,则BM=CN.
证明:在图三中,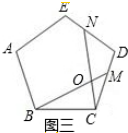
∵五边形ABCDE是正五边形,
∴BC=CD,∠BCM=∠CDN=108°.
∵∠BON=108°,
∴∠CBM+∠BCN=108°.
∵∠BCN+∠DCN=108°,
∴∠CBM=∠DCN.
∴△BCM≌△CDN(ASA).
∴BM=CN
点评 本题主要考查了全等三角形,正多边形等几何知识,是一道几何型探究题.很好地体现了从一般到特殊的数学思想方法,引导学生渐渐地从易走到难.


科目:初中数学 来源: 题型:解答题
 小强为了测量一幢高楼高AB,在旗杆CD与楼之间选定一点P.测得旗杆顶C视线PC与地面夹角∠DPC=36°,测楼顶A视线PA与地面夹角∠APB=54°,量得P到楼底距离PB与旗杆高度相等,等于10米,量得旗杆与楼之间距离为DB=36米,小强计算出了楼高,楼高AB是多少米?
小强为了测量一幢高楼高AB,在旗杆CD与楼之间选定一点P.测得旗杆顶C视线PC与地面夹角∠DPC=36°,测楼顶A视线PA与地面夹角∠APB=54°,量得P到楼底距离PB与旗杆高度相等,等于10米,量得旗杆与楼之间距离为DB=36米,小强计算出了楼高,楼高AB是多少米?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
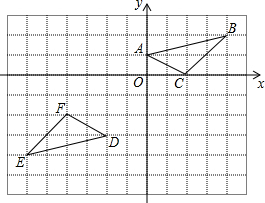 如图,在平面直角坐标系中,将△ABC绕点P旋转180°得到△DEF,则点P的坐标为( )
如图,在平面直角坐标系中,将△ABC绕点P旋转180°得到△DEF,则点P的坐标为( )| A. | (-1,0) | B. | (-1,-1) | C. | (-2,-1) | D. | (-2,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
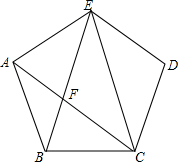 如图,正五边形ABCDE中,连接EC,AC,BE,且AC和BE交于点F,则F为AC的黄金分割点.那么△ABF和△ECF的面积之比为=$\frac{3-\sqrt{5}}{2}$.
如图,正五边形ABCDE中,连接EC,AC,BE,且AC和BE交于点F,则F为AC的黄金分割点.那么△ABF和△ECF的面积之比为=$\frac{3-\sqrt{5}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com