
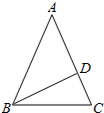
 如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,下列结论中:
如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,下列结论中:分析 在△ABC,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,可推出△BCD,△ABD为等腰三角形,可得AD=BD=BC,①正确;由三角形的面积公式得出②正确;利用三角形相似的判定与性质得出③④正确,即可得出结果.
解答 解:①由AB=AC,∠A=36°,得∠ABC=∠C=72°,
又BD平分∠ABC交AC于点D,
∴∠ABD=∠CBD=$\frac{1}{2}$∠ABC=36°=∠A,
∴AD=BD,
∠BDC=∠ABD+∠A=72°=∠C,
∴BC=BD,
∴BC=BD=AD,
∴①正确;
②△ABD与△BCD在AC边上的高相等,
故△ABD与△BCD的面积比等于对应底边的比,
∴②正确;
③由①的条件可证△BCD∽△ACB,
则BC:AC=CD:BC,
∴BC2=CD•AC,
∴③正确;
④设BC=x,则AC=AB=2,CD=AC-AD=2-x,
由BC2=CD•AC,得x2=(2-x)•2,
解得x=±$\sqrt{5}$-1(舍去负值),
∴BC=$\sqrt{5}$-1,
∴④正确.
正确的有4个,
故答案为:4.
点评 本题考查了等腰三角形的判定与性质,相似三角形判定与性质.明确图形中的三个等腰三角形的特点与关系是解决问题的关键.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:解答题
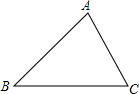 如图,已知△ABC中,AC=6,∠ABC=45°.
如图,已知△ABC中,AC=6,∠ABC=45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 组别 | 正确字数x | 人数 |
| A | 0≤x<10 | 10 |
| B | 10≤x<20 | 15 |
| C | 20≤x<30 | 25 |
| D | 30≤x<40 | m |
| E | 40≤x<50 | n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com