
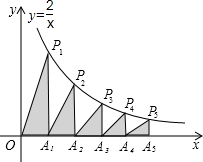
 如图,在x轴的正半轴上依次截取OA1=A1A2=A2A3=A3A4=A4A5,过点A1、A2、A3、A4、A5分别作x轴的垂线与反比例函数y=$\frac{2}{x}$(x≠0)的图象相交于点P1、P2、P3、P4、P5,得直角三角形OP1A1、A1P2A2、A2P3A3、A3P3A4、A4P5A5,并设其面积分别为S1、S2、S3、S4、S5,则S5的值为( )
如图,在x轴的正半轴上依次截取OA1=A1A2=A2A3=A3A4=A4A5,过点A1、A2、A3、A4、A5分别作x轴的垂线与反比例函数y=$\frac{2}{x}$(x≠0)的图象相交于点P1、P2、P3、P4、P5,得直角三角形OP1A1、A1P2A2、A2P3A3、A3P3A4、A4P5A5,并设其面积分别为S1、S2、S3、S4、S5,则S5的值为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{5}$ |
分析 根据反比例函数y=$\frac{k}{x}$中k的几何意义再结合图象即可解答.
解答 解:∵过双曲线上任意一点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S是个定值,S=$\frac{1}{2}$|k|.
∴S1=1,S△OA2P2=1,
∵OA1=A1A2,
∴$\frac{1}{2}$S△OA2P2=$\frac{1}{2}$,
同理可得,S2=$\frac{1}{2}$S1=$\frac{1}{2}$,S3=$\frac{1}{3}$S1=$\frac{1}{3}$,S4=$\frac{1}{4}$S1=$\frac{1}{4}$,S5=$\frac{1}{5}$S1=$\frac{1}{5}$.
故选D.
点评 主要考查了反比例函数y=$\frac{k}{x}$中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点;这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=$\frac{1}{2}$|k|.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
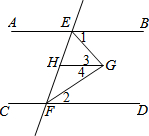 完成下面的证明:
完成下面的证明:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
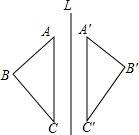 如图,△ABC与△A′B′C′关于直线L对称,若∠A=60°,∠C′=45°,则∠B的度数是( )
如图,△ABC与△A′B′C′关于直线L对称,若∠A=60°,∠C′=45°,则∠B的度数是( )| A. | 105° | B. | 75° | C. | 60° | D. | 45° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
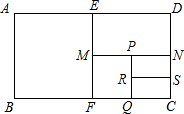 如图,在矩形ABCD中,AB=a,将矩形ABCD沿EF对折后,得ABFE和矩形EFCD,然后再把其中的一个矩形EFCD沿MN对折,得矩形MNCF和矩形MNDE,…,依此类推,得矩形PRSN和RQCS,并且所有矩形都相似,则RS等于( )
如图,在矩形ABCD中,AB=a,将矩形ABCD沿EF对折后,得ABFE和矩形EFCD,然后再把其中的一个矩形EFCD沿MN对折,得矩形MNCF和矩形MNDE,…,依此类推,得矩形PRSN和RQCS,并且所有矩形都相似,则RS等于( )| A. | $\frac{\sqrt{2}}{8}$a | B. | $\frac{\sqrt{2}}{4}$a | C. | $\frac{\sqrt{2}}{2}$a | D. | $\frac{1}{4}$a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com