练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如果关于x的一元二次方程x2﹣kx+2＝0中，k是投掷骰子所得的数字（1，2，3，4，5，6），则该二次方程有两个不等实数根的概率为（　　）

    A. B. C. D.

    【答案】A

    【解析】

    首先根据题意计算出所有基本事件总数，然后根据题意求出一元二次方程具有两个不等实数根时所包含的基本事件数，进而计算出答案．

    二次方程有两个不等实数根，由根的判别式可得 k2-8＞0，

    k=1，k2-8=-7，不符合题意；

    k=2，k2-8=-4，不符合题意，

    k=3，k2-8=1，符合题意，

    k=4，k2-8=8，符合题意；

    k=5，k2-8=17，符合题意；

    k=6，k2-8=28，符合题意．

    共有6种等可能的结果，4种符合题意，根的概率是：，

    故选A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图①，在△ABC中，∠C=90°，AC=8cm，BC=6cm．动点P在线段AC上以5cm/s的速度从点A运动到点C．过点P作PD⊥AB于点D，将△APD绕PD的中点旋转180°得到△A'DP．设点P的运动时间为x(s)．

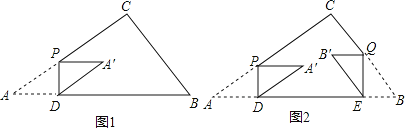
    (1)求点A'落在边BC上时x的值．

    (2)设△A'DP和△ABC重叠部分图形周长为y(cm)，求y与x之间的函数关系式．

    (3)如图②，另有一动点Q与点P同时出发，在线段BC上以5cm/s的速度从点B运动到点C．过点Q作QE⊥AB于点E，将△BQE绕QE的中点旋转180°得到△B'EQ．连结A′B′．当直线A'B'与△ABC的边垂直或平行时，直接写出x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点在直线上，点的坐标分别是，连接，将沿射线方向平移，使点O移动到点M，得到（点分别对应点）.

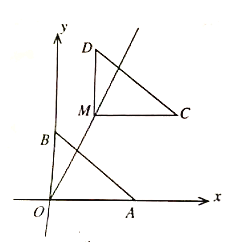
    （1）填空：m的值为_____________，点C的坐标是______________；

    （2）在射线上是否存在一点N，使，如果存在，请求出点N的坐标；如果不存在，请说明理由；

    （3）连接，点P是射线上一动点，请直接写出使是等腰三角形时点P的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】春节期间，根据习俗每家每户都会在门口挂灯笼和对联，某商店看准了商机，购进了一批红灯笼和对联进行销售，已知每幅对联的进价比每个红灯笼的进价少10元，且用480元购进对联的幅数是用同样金额购进红灯笼个数的6倍．

    （1）求每幅对联和每个红灯笼的进价分别是多少？

    （2）由于销售火爆，第一批销售完了以后，该商店用相同的价格再购进300幅对联和200个红灯笼，已知对联售价为6元一幅，红灯笼售价为24元一个，销售一段时间后，对联卖出了总数的，红灯笼售出了总数的，为了清仓，该店老板对剩下的对联和红灯笼以相同的折扣数进行打折销售，并很快全部售出，求商店最低打几折可以使得这批货的总利润率不低于90%？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知如图，D是△ABC中AB边上的中点，△ACE和△BCF分别是以AC、BC为斜边的等腰直角三角形，连接DE、DF．

    求证：DE=DF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

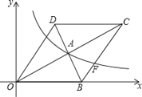
    【题目】如图，在平面直角坐标系中，菱形OBCD的边OB在x轴上，反比例函数y=（x＞0）的图象经过菱形对角线的交点A，且与边BC交于点F，点A的坐标为（4，2）．

    （1）求反比例函数的表达式；

    （2）求BC所在直线的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】两幢大楼的部分截面及相关数据如图，小明在甲楼A处透过窗户E发现乙楼F处出现火灾，此时A,E,F在同一直线上.跑到一楼时，消防员正在进行喷水灭火，水流路线呈抛物线，在1.2m高的D处喷出，水流正好经过E,F. 若点B和点E、点C和F的离地高度分别相同，现消防员将水流抛物线向上平移0.4m，再向左后退了____m，恰好把水喷到F处进行灭火．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校开展拓展课程展示活动，需要制作A，B两种型号的宣传广告共20个，已知A，B两种广告牌的单价分别为40元，70元

    （1）若根据活动需要，A种广告牌数量与B种广告牌数量之比为3：2，需要多少费用？

    （2）若需制作A，B两种型号的宣传广告牌，其中B种型号不少于5个，制作总费用不超过1000元，则有几种制作方案？每一种制作方案的费用分别是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（问题提出）|a﹣1|+|a﹣2|+|a﹣3|+…+|a﹣2019|最小值是多少？

    （阅读理解）

    为了解决这个问题，我们先从最简单的情况入手．|a|的几何意义是a这个数在数轴上对应的点到原点的距离．那么|a﹣1|可以看做a这个数在数轴上对应的点到1的距离；|a﹣1|+|a﹣2|就可以看作a这个数在数轴上对应的点到1和2两个点的距离之和．下面我们结合数轴研究|a﹣1|+|a﹣2|的最小值．

    我们先看a表示的点可能的3种情况，如图所示：

    （1）如图①，a在1的左边，从图中很明显可以看出a到1和2的距离之和大于1．

    （2）如图②，a在1和2之间（包括在1，2上），可以看出a到1和2的距离之和等于1．

    （3）如图③，a在2的右边，从图中很明显可以看出a到1和2的距离之和大于1．

    （问题解决）

    （1）|a﹣2|+|a﹣5|的几何意义是　 　．请你结合数轴探究：|a﹣2|+|a﹣5|的最小值是　 　．

    （2）|a﹣1|+|a﹣2|+|a﹣3|的几何意义是　 　．请你结合数轴探究：|a﹣1|+|a﹣2|+|a﹣3|的最小值是　 　，并在图④的数轴上描出得到最小值时a所在的位置，由此可以得出a为　 　．

    （3）求出|a﹣1|+|a﹣2|+|a﹣3|+|a﹣4|+|a﹣5|的最小值．

    （4）求出|a﹣1|+|a﹣2|+|a﹣3|+…+|a﹣2019|的最小值．

    （拓展应用）

    请在图⑤的数轴上表示出a，使它到2，5的距离之和小于4，并直接写出a的范围．

    查看答案和解析>>

    同步练习册答案