
����Ŀ����ͼ��������y=![]() +bx+c��x�ύ��A��1��0����B����4��0�����㣬
+bx+c��x�ύ��A��1��0����B����4��0�����㣬
��1����������ߵĽ���ʽ��
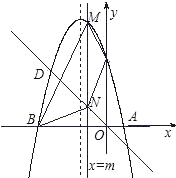
��2���裨1���е������߽�y����C�㣬�ڸ������ߵĶԳ������Ƿ���ڵ�Q��ʹ����QAC���ܳ���С�������ڣ����Q������ꣻ�������ڣ���˵�����ɣ�
��3�������������ֱ��y=��x�ڵڶ������ڵ�D��ƽ����y���ֱ��x=m��(![]() )�������߽��ڵ�M����ֱ��y=��x���ڵ�N������BM��CM��NC��NB���Ƿ����m��ֵ��ʹ�ı���BNCM�����S��������ڣ������m��ֵ���������ڣ���˵�����ɣ�
)�������߽��ڵ�M����ֱ��y=��x���ڵ�N������BM��CM��NC��NB���Ƿ����m��ֵ��ʹ�ı���BNCM�����S��������ڣ������m��ֵ���������ڣ���˵�����ɣ�

���𰸡���1��y=![]() ��3x+4��(2)���ڣ��ڸ������ߵĶԳ����ϴ��ڵ�Q����1.5��2.5����ʹ����QAC���ܳ���С����3�����ڣ�m=-1.
��3x+4��(2)���ڣ��ڸ������ߵĶԳ����ϴ��ڵ�Q����1.5��2.5����ʹ����QAC���ܳ���С����3�����ڣ�m=-1.
��������
�����������1��A��B���������������y=![]() +bx+cȷ������ʽ��
+bx+cȷ������ʽ��
��2��A��B���ڶԳ���Գƣ�BC��Գ���Ľ�����ǵ�Q��
��3���ı���BNCM�����������MNB�����+��MNC�������
�����������1����������y=![]() +bx+c��x�ύ��A��1��0����B����4��0�����㣬
+bx+c��x�ύ��A��1��0����B����4��0�����㣬
��A��B����������������߷��̣���![]() �����
�����![]() ��
��
���ԣ��������ߵĽ���ʽΪ��y=![]() ��3x+4��
��3x+4��
��2�����ڣ��������£�
����ǰ��ļ�����Եõ���C��0��4�����������ߵĶԳ���Ϊֱ��x=��1.5��
���������ߵĶԳ��ԣ���A��B����ֱ��x=1�Գƣ�
����QC+QA��Сʱ����QAC���ܳ�����С��
������Q��ֱ��BC��ʱQC+QA��С��
��ʱֱ��BC�Ľ���ʽΪy=x+4��
��x=��1.5ʱ��y=2.5��
���ڸ������ߵĶԳ����ϴ��ڵ�Q����1.5��2.5����ʹ����QAC���ܳ���С��
��3�������⣬M��m��![]() ��3m+4����N��m����m����
��3m+4����N��m����m����
���߶�MN=![]() ��3m+4������m��=
��3m+4������m��=![]() ��2m+4=
��2m+4=![]() +5��
+5��
��![]() =0.5MN��BO=2MN=
=0.5MN��BO=2MN=![]() +10��
+10��
����m=��1ʱ����![]() �ڣ����ı���BNCM�����S���
�ڣ����ı���BNCM�����S���


 ����������������ϵ�д�
����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�κ���y=kx+b����x��ֵ��С1ʱ��y��ֵ��С2����x��ֵ����2ʱ��y��ֵ________4.��ѡ����������������С����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ������ͼ���������������߶��У�����߶γ�Ϊ�������ͼ�ε�ֱ�������ݴ˶��壬ͼ�����Ρ����Ρ�ֱ�����Ρ���ʮ��ͼ�꣩�С�ֱ������С���ǣ� ��.
A�� B��
B�� C��
C�� D��
D��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪x1=3�ǹ���x��һԪ���η���x2-4x+c=0��һ�������̵���һ����x2����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������и����ֱ�������Ӧ�ĺ����ϣ�
1��-0.20�� ![]() ��325��-789��0��-23.13��0.618��-2014����0.1010010001����
��325��-789��0��-23.13��0.618��-2014����0.1010010001����
��������
��������
��������
����������
����������
����������
�Ǹ����У���
����������
�Ǹ������У� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������1.31��108��ȷ���� ��
A. �ٷ�λ B. ʮ��λ C. ǧ��λ D. ����λ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
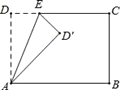
����Ŀ����ͼ��������ABCD�У���DAB=��B=��C=��D=90����AD=BC=9��AB=CD=15����EΪ����DC�ϵ�һ�����㣬��ADE����AD��E����ֱ��AE�Գƣ�����AD��BΪֱ��������ʱ��DEΪ_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����һ����ѧ�⣺����֪��������ʽA��B��BΪ ![]() ��5x��6����A+B����С����A+B����A��B����������
��5x��6����A+B����С����A+B����A��B���������� ![]() +10x+12������������Ϣ���������A+B�Ľ����
+10x+12������������Ϣ���������A+B�Ľ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com