
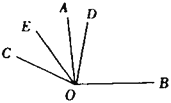
【题目】如图,已知同一平面内![]() ,
,![]() .
.
(1)问题发现:![]() 的余角是_____,
的余角是_____,![]() 的度数是_____;
的度数是_____;
(2)拓展探究:若![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,则
,则![]() 的度数是_____.
的度数是_____.
(3)类比延伸:在(2)的条件下,如果将题目中的![]() 改为
改为![]() ;
;![]() 改为
改为![]() ,其他条件不变,你能求出
,其他条件不变,你能求出![]() 吗?若能,请你写出求解过程;若不能,请说明理由.
吗?若能,请你写出求解过程;若不能,请说明理由.
【答案】(1)∠AOD,150°;(2)45°;(3)![]() =
=![]()
【解析】
(1)根据题意可得∠BOD+∠AOD=90°,即可得到![]() 的余角,根据
的余角,根据![]() ,
,![]() 即可求出
即可求出![]() ;
;
(2)由(1)的结论可求∠COD=75°,根据![]() 平分
平分![]() 可求∠COE=30°,由此可计算得出
可求∠COE=30°,由此可计算得出![]() 的度数;
的度数;
(3)先求出∠BOC=![]() ,类比(2)的方法求解即可.
,类比(2)的方法求解即可.
(1)∵![]() ,
,
∴∠BOD+∠AOD=90°,
∴![]() 的余角是∠AOD,
的余角是∠AOD,
∵![]() ,
,![]() ,
,
∴![]() =∠AOB+∠AOC=150°,
=∠AOB+∠AOC=150°,
故答案为:∠AOD,150°;
(2)由(1)知![]() =150°,
=150°,
∵![]() 平分
平分![]() ,
,
∴∠COD=75°,
∵![]() 平分
平分![]() ,
,
∴∠COE=30°,
∴![]() =∠COD-∠COE=45°,
=∠COD-∠COE=45°,
故答案为:45°;
(3)能求出![]() 的度数,
的度数,
∵![]() ,
,![]() ,
,
∴∠BOC=![]()
∵![]() 平分
平分![]() ,
,![]() ,
,
∴∠COD=![]() ,
,
∵![]() 平分
平分![]() ,
,![]()
∴∠COE=![]() ,
,
∴![]() =∠COD-∠COE=
=∠COD-∠COE=![]() .
.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】如图,等边△ABC中,AD是∠BAC的角平分线,E为AD上一点,以BE为一边且在BE下方作等边△BEF,连接CF.

(1)求证:AE=CF;
(2)求∠ACF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC为等腰三角形,AB=AC,点D为直线BC上一动点(点D不与点B、点C重合).以AD为边作△ADE,且AD=AE,连接CE,∠BAC=∠DAE.
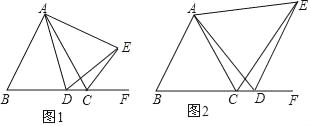
(1)如图1,当点D在边BC上时,试说明:①△ABD≌△ACE;②BC=DC+CE;
(2)如图2,当点D在边BC的延长线上时,其他条件不变,探究线段BC、DC、CE之间存在的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,贵阳市某中学数学活动小组在学习了“利用三角函数测高”后.选定测量小河对岸一幢建筑物BC的高度.他们先在斜坡上的D处,测得建筑物顶的仰角为30°.且D离地面的高度DE=5m.坡底EA=10m,然后在A处测得建筑物顶B的仰角是50°,点E,A,C在同一水平线上,求建筑物BC的高.(结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人的大脑所能记忆的内容是有限的,随着时间的推移,记忆的东西会逐渐被遗忘.教乐乐数学的马老师调查了自己班学生的学习遗忘规律,并根据调查数据描绘了一条曲线(如图所示),其中纵轴表示学习中的记忆保持量,横轴表示时间,观察图象并回答下列问题:

(1)观察图象,![]() 后,记忆保持量约为 ;
后,记忆保持量约为 ;![]() 后,记忆保持量约为 ;
后,记忆保持量约为 ;
(2)图中的![]() 点表示的意义是什么?
点表示的意义是什么?
![]() 点表示的意义是 ;
点表示的意义是 ;
在以下哪个时间段内遗忘的速度最快?填序号 ;
①0—2![]() ;②2—4
;②2—4![]() ; ③4—6
; ③4—6![]() ; ④6—8
; ④6—8![]()
(3)马老师每节课结束时都会对本节课进行总结回顾,并要求学生每天晚上临睡前对当天课堂上所记的课堂笔记进行复习,据调查这样一天后记忆量能保持98%,如果学生一天不复习,结果又会怎样?由此,你能根据上述曲线规律制定出两条今年暑假的学习计划吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图甲,AB∥CD,试问∠2与∠1+∠3的关系是什么,为什么?
(2)如图乙,AB∥CD,试问∠2+∠4与∠1+∠3+∠5一样大吗?为什么?
(3)如图丙,AB∥CD,试问∠2+∠4+∠6与∠1+∠3+∠5+∠7哪个大?为什么?
你能将它们推广到一般情况吗?请写出你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣(x﹣1)2+c与x轴交于A,B(A,B分别在y轴的左右两侧)两点,与y轴的正半轴交于点C,顶点为D,已知A(﹣1,0).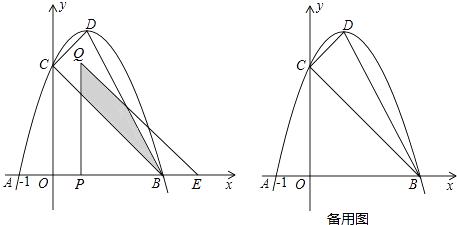
(1)求点B,C的坐标;
(2)判断△CDB的形状并说明理由;
(3)将△COB沿x轴向右平移t个单位长度(0<t<3)得到△QPE.△QPE与△CDB重叠部分(如图中阴影部分)面积为S,求S与t的函数关系式,并写出自变量t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,过点A(﹣ ![]() ,0)的两条直线分别交y轴于B,C两点,且B,C两点的纵坐标分别是一元二次方程x2﹣2x﹣3=0的两个根.
,0)的两条直线分别交y轴于B,C两点,且B,C两点的纵坐标分别是一元二次方程x2﹣2x﹣3=0的两个根.
(1)求线段BC的长度;
(2)试问:直线AC与直线AB是否垂直?请说明理由;
(3)若点D在直线AC上,且DB=DC,求点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com