
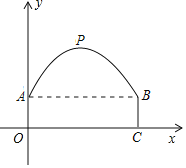
【题目】如下图,隧道的截面由抛物线和矩形构成,![]() ,隧道的最高点P位于AB的中点的正上方,且与AB的距离为4m.
,隧道的最高点P位于AB的中点的正上方,且与AB的距离为4m.
![]() 建立如图所示的坐标系,求图中抛物线的解析式;
建立如图所示的坐标系,求图中抛物线的解析式;
![]() 若隧道为单向通行,一辆高4米、宽3米的火车能否从隧道内通过?请说明理由.
若隧道为单向通行,一辆高4米、宽3米的火车能否从隧道内通过?请说明理由.
科目:初中数学 来源: 题型:
【题目】2018年5月5日,中国邮政发行《马克思诞辰200周年》纪念邮票1套2枚(如图),这套邮票正面图案为:马克思像、马克思与恩格斯像,背面完全相同.发行当日,小宇购买了此款纪念邮票2套,他将2套邮票沿中间虚线撕开(使4枚形状、大小完全相同)后将4枚纪念邮票背面朝上放在桌面上,并随机从中抽出2张,则抽出的2张邮票恰好都是“马克思像”的概率为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,且AB=12,点C为半圆上的一点.将此半圆沿BC所在的直线折叠,若圆弧BC恰好过圆心O,则图中阴影部分的面积是( )

A. 4πB. 5πC. 6πD. 8π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AB=4,△BCD为等边三角形,点E为△BCD围成的区域(包括各边)内的一点,过点E作EM∥AB,交直线AC于点M,作EN∥AC,交直线AB于点N,则![]() AN+AM的最大值为_____.
AN+AM的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,⊙C的圆心坐标为(1,0),半径为1,![]() 为⊙C的直径,若点
为⊙C的直径,若点![]() 的坐标为(a,b)则点
的坐标为(a,b)则点![]() 的坐标为( )
的坐标为( )
A.(-a-1,-b)B.(-a+1,-b)C.(-a+2,-b)D.(-a-2,-b)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣![]() x2+
x2+![]() x﹣1与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,其顶点为D.将抛物线位于直线l:y=t(t<
x﹣1与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,其顶点为D.将抛物线位于直线l:y=t(t<![]() )上方的部分沿直线l向下翻折,抛物线剩余部分与翻折后所得图形组成一个“M”形的新图象.
)上方的部分沿直线l向下翻折,抛物线剩余部分与翻折后所得图形组成一个“M”形的新图象.
(1)点A,B,D的坐标分别为 , , ;
(2)如图①,抛物线翻折后,点D落在点E处.当点E在△ABC内(含边界)时,求t的取值范围;
(3)如图②,当t=0时,若Q是“M”形新图象上一动点,是否存在以CQ为直径的圆与x轴相切于点P?若存在,求出点P的坐标;若不存在,请说明理由.
[Failed to download image : http://192.168.0.10:8086/QBM/2019/5/28/2213337932849152/2214008649842688/STEM/890e59b444e5404588b8511540e03e41.png]
查看答案和解析>>
科目:初中数学 来源: 题型:
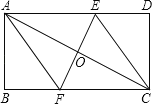
【题目】已知如图,矩形ABCD的周长为64,AB=12,对角线AC的垂直平分线分别交AD、BC于E、F,连接AF、CE、EF,且EF与AC相交于点O.
(1)求证:四边形AECF是菱形;
(2)求S△ABF与S△AEF的比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a>0)的顶点为M,直线y=m与抛物线交于点A,B,若△AMB为等腰直角三角形,我们把抛物线上A,B两点之间的部分与线段AB 围成的图形称为该抛物线对应的准蝶形,线段AB称为碟宽,顶点M 称为碟顶.

(1)由定义知,取AB中点N,连结MN,MN与AB的关系是_____.
(2)抛物线y=![]() 对应的准蝶形必经过B(m,m),则m=_____,对应的碟宽AB是_____.
对应的准蝶形必经过B(m,m),则m=_____,对应的碟宽AB是_____.
(3)抛物线y=ax2﹣4a﹣![]() (a>0)对应的碟宽在x 轴上,且AB=6.
(a>0)对应的碟宽在x 轴上,且AB=6.
①求抛物线的解析式;
②在此抛物线的对称轴上是否有这样的点P(xp,yp),使得∠APB为锐角,若有,请求出yp的取值范围.若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果点D、E分别在△ABC中的边AB和AC上,那么不能判定DE∥BC的比例式是( )
A. AD:DB=AE:EC B. DE:BC=AD:AB
C. BD:AB=CE:AC D. AB:AC=AD:AE
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com