
 在平面直角坐标系xOy中,一次函数y=ax+b(a≠0)的图象与反比例函数y=
在平面直角坐标系xOy中,一次函数y=ax+b(a≠0)的图象与反比例函数y=| k |
| x |
| 2 |
| 5 |
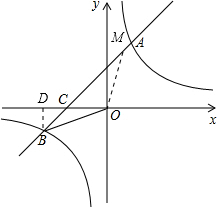 解:如图过点B作BD⊥x轴,交x轴于点D,
解:如图过点B作BD⊥x轴,交x轴于点D,| BD |
| OD |
| 2 |
| 5 |
| 2 |
| -n |
| 2 |
| 5 |
|
|
| x2+(x+3)2 |
| OD2+BD2 |
| 52+22 |
| 29 |
| 2 |
| OM |
| OC |
| BO |
| BC |
| ||
| 3 |
| ||
2
|
| 1 |
| 4 |
| 51 |
| 3 |
| 2 |
| 1 |
| 4 |
| 51 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 4 |
| 51 |
| 1 |
| 4 |
| 51 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 4 |
| 51 |
| 1 |
| 4 |
| 51 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 4 |
| 51 |
| 1 |
| 4 |
| 51 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 4 |
| 51 |


科目:初中数学 来源: 题型:
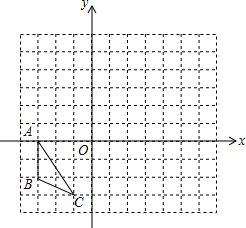 如图,在边长为1的正方网格内有一个三角形ABC.
如图,在边长为1的正方网格内有一个三角形ABC.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
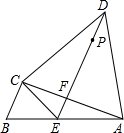 某小区有A、B、C、D四栋居民楼,经测量发现A、C、D三栋居民楼两两距离相等,且∠ACB=90°,物业打算在A、B两楼之间的小路AB上修建一个休闲运动区域E,且D楼居民恰好能沿着小路DE直达该区域,小路DE和小路AC恰好互相垂直,垂足为F.
某小区有A、B、C、D四栋居民楼,经测量发现A、C、D三栋居民楼两两距离相等,且∠ACB=90°,物业打算在A、B两楼之间的小路AB上修建一个休闲运动区域E,且D楼居民恰好能沿着小路DE直达该区域,小路DE和小路AC恰好互相垂直,垂足为F.查看答案和解析>>
科目:初中数学 来源: 题型:
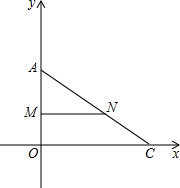 如图,平面直角坐标系中,点A,C两点分别在x轴和y轴上,点A的坐标点(0,6),点C的坐标(8,0),M、N分别为OA、AC的中点,动点P从O出发以每秒1个单位的速度沿折线OCNM运动,以P为圆心,以3为半径作⊙P,以N为圆心,以1为半径作⊙N.
如图,平面直角坐标系中,点A,C两点分别在x轴和y轴上,点A的坐标点(0,6),点C的坐标(8,0),M、N分别为OA、AC的中点,动点P从O出发以每秒1个单位的速度沿折线OCNM运动,以P为圆心,以3为半径作⊙P,以N为圆心,以1为半径作⊙N.查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com