
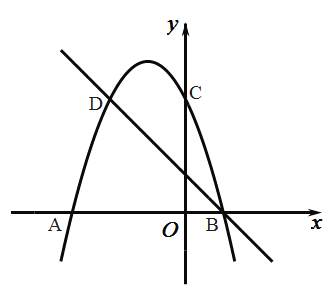
【题目】如图二次函数的图象与![]() 轴交于点
轴交于点![]() 和
和![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 、
、![]() 是二次函数图象上的一对对称点,一次函数的图象经过
是二次函数图象上的一对对称点,一次函数的图象经过![]() 、
、![]()
(1)求二次函数的解析式;
(2)写出使一次函数值大于二次函数值的![]() 的取值范围;
的取值范围;
(3)若直线![]() 与
与![]() 轴的交点为
轴的交点为![]() 点,连结
点,连结![]() 、
、![]() ,求
,求![]() 的面积;
的面积;
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)4.
;(3)4.
【解析】
(1)直接将已知点代入函数解析式求出即可;
(2)利用函数图象结合交点坐标得出使一次函数值大于二次函数值的x的取值范围;
(3)分别得出EO,AB的长,进而得出面积.
(1)∵二次函数与![]() 轴的交点为
轴的交点为![]() 和
和![]()
∴设二次函数的解析式为:![]()
∵![]() 在抛物线上,
在抛物线上,
∴3=a(0+3)(0-1),
解得a=-1,
所以解析式为:![]() ;
;
(2)![]() =x22x+3,
=x22x+3,
∴二次函数的对称轴为直线![]() ;
;
∵点![]() 、
、![]() 是二次函数图象上的一对对称点;
是二次函数图象上的一对对称点;![]()
∴![]() ;
;
∴使一次函数大于二次函数的![]() 的取值范围为
的取值范围为![]() 或
或![]() ;
;
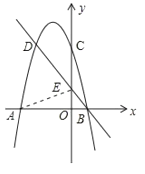
(3)设直线BD:y=mx+n,
代入B(1,0),D(2,3)得![]() ,
,
解得:![]() ,
,
故直线BD的解析式为:y=x+1,
把x=0代入![]() 得,y=3,
得,y=3,
所以E(0,1),
∴OE=1,
又∵AB=4,
∴S△ADE=![]() ×4×3
×4×3![]() ×4×1=4.
×4×1=4.


科目:初中数学 来源: 题型:
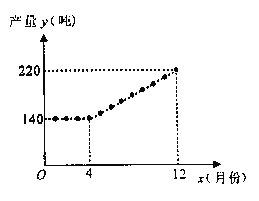
【题目】非洲猪瘟疫情发生以来,猪肉市场供应阶段性偏紧和猪价大幅波动时有发生,为稳定生猪生产,促进转型升级,增强猪肉供应保障能力,国务院办公厅于2019年9月印发了《关于稳定生猪生产促进转型升级的意见》,某生猪饲养场积极响应国家号召,努力提高生产经营管理水平,稳步扩大养殖规模,增加猪肉供应量。该饲养场2019年每月生猪产量y(吨)与月份x(![]() ,且x为整数)之间的函数关系如图所示.
,且x为整数)之间的函数关系如图所示.
(1)请直接写出当![]() (x为整数)和
(x为整数)和![]() (x为整数)时,y与x的函数关系式;
(x为整数)时,y与x的函数关系式;
(2)若该饲养场生猪利润P(万元/吨)与月份x(![]() ,且x为整数)满足关系式:
,且x为整数)满足关系式:![]() ,请问:该饲养场哪个月的利润最大?最大利润是多少?
,请问:该饲养场哪个月的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°.
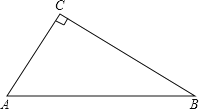
(1)利用尺规作图,在BC边上求作一点P,使得点P到边AB的距离等于PC的长;(要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)
(2)在(1)的条件下,以点P为圆心,PC长为半径的⊙P中,⊙P与边BC相交于点D,若AC=6,PC=3,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系![]() 中,
中,![]() 、
、![]() ,将
,将![]() 经过旋转、平移变化后得到如图1所示的
经过旋转、平移变化后得到如图1所示的![]() .
.
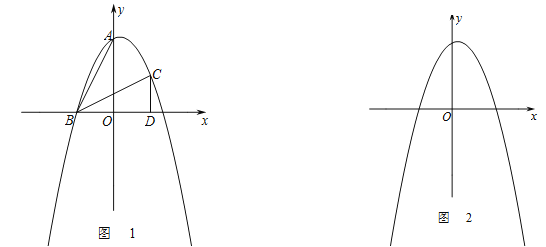
(1)求经过![]() 、
、![]() 、
、![]() 三点的抛物线的解析式;
三点的抛物线的解析式;
(2)连结![]() ,点
,点![]() 是位于线段
是位于线段![]() 上方的抛物线上一动点,若直线
上方的抛物线上一动点,若直线![]() 将
将![]() 的面积分成
的面积分成![]() 两部分,求此时点
两部分,求此时点![]() 的坐标;
的坐标;
(3)现将![]() 、
、![]() 分别向下、向左以
分别向下、向左以![]() 的速度同时平移,求出在此运动过程中
的速度同时平移,求出在此运动过程中![]() 与
与![]() 重叠部分面积的最大值.
重叠部分面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某山区不仅有美丽风光,也有许多令人喜爱的土特产,为实现脱贫奔小康,某村组织村民加工包装土特产销售给游客,以增加村民收入.已知某种士特产每袋成本10元.试销阶段每袋的销售价x(元)与该士特产的日销售量y(袋)之间的关系如表:
x(元) | 15 | 20 | 30 | … |
y(袋) | 25 | 20 | 10 | … |
若日销售量y是销售价x的一次函数,试求:
(1)日销售量y(袋)与销售价x(元)的函数关系式;
(2)假设后续销售情况与试销阶段效果相同,要使这种土特产每日销售的利润最大,每袋的销售价应定为多少元?每日销售的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠ABC=90°,AB=BC.直线l与以BC为直径的圆O相切于点C.点F是圆O上异于B、C的动点,直线BF与l相交于点E,过点F作AF的垂线交直线BC与点D.
(1)如果BE=15,CE=9,求EF的长;
(2)证明:①△CDF∽△BAF;②CD=CE;
(3)探求动点F在什么位置时,相应的点D位于线段BC的延长线上,且使BC=![]() CD,请说明你的理由.
CD,请说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
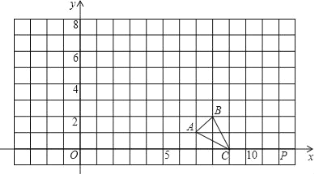
【题目】在直角坐标系中△ABC三个顶点坐标分别为A(7,1)、B(8,2)、C(9,0).
(1)请在图中画出△ABC的一个以点P (12,0)为位似中心,相似比为3的位似图形△A′B′C′(要求与△ABC同在P点一侧);
(2)请直接写出点B′及点C′的坐标;
(3)求线段BC的对应线段B′C′所在直线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
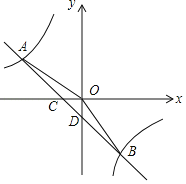
【题目】如图,在平面直角坐标系中,一次函数y=ax+b的图象与反比例函数y=![]() 的图象交于第二、四象限内的A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,﹣4),连接AO,AO=5,sin∠AOC=
的图象交于第二、四象限内的A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,﹣4),连接AO,AO=5,sin∠AOC=![]() .
.
(1)求反比例函数和一次函数的解析式;
(2)连接OB,求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应新旧动能转换.提高公司经济效益.某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为40万元时,年销售量为600台;每台售价为45万元时,年销售量为550台.假定该设备的年销售量y(单位:台)和销售单价![]() (单位:万元)成一次函数关系.
(单位:万元)成一次函数关系.
(1)求年销售量![]() 与销售单价
与销售单价![]() 的函数关系式;
的函数关系式;
(2)根据相关规定,此设备的销售单价不得高于70万元,如果该公司想获得10000万元的年利润.则该设备的销售单价应是多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com