练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

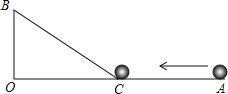
    【题目】如图，∠AOB=90°，OA=45cm，OB=15cm，一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O，机器人立即从点B出发，沿直线匀速前进拦截小球，恰好在点C处截住了小球．如果小球滚动的速度与机器人行走的速度相等，那么机器人行走的路程BC是多少？

    【答案】25cm.

    【解析】

    试题本题考查勾股定理的实际应用问题，结合了物理知识以及小球的动态变化，根据题意可以直到小球滚动的速度与机器人行走的速度相等，运动时间相等，得出BC=AC，由勾股定理可求得BC的长．

    试题解析：∵小球滚动的速度与机器人行走的速度相等，运动时间相等，

    即BC=CA，设AC为x，则OC=45-x， 由勾股定理可知OB2+OC2=BC2，

    又∵OA=45，OB=15， 把它代入关系式152+（45-x）2=x2，

    解方程得出x=25（cm）．

    答：如果小球滚动的速度与机器人行走的速度相等，那么机器人行走的路程BC是25cm．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】小华通过学习函数发现：若二次函数y=ax2+bx+c（a≠0）的图象经过点（x1 ， y1），（x2 ， y2）（x1＜x2），若y1y2＜0，则方程ax2+bx+c=0（a≠0）的一个根x0的取值范围是x1＜x0＜x2 ， 请你类比此方法，推断方程x3+x﹣1=0的实数根x0所在范围为（ ）
    A.﹣ ＜x0＜0
    B.0＜x0＜
    C. ＜x0＜1
    D.1＜x0＜

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了解当地气温变化情况，某研究小组记录了寒假期间连续6天的最高气温，结果如下（单位：℃）：﹣6，﹣3，x，2，﹣1，3，若这组数据的中位数是﹣1，在下列结论中：①方差是8；②极差是9；③众数是﹣1；④平均数是﹣1，其中正确的序号是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知点A、D、C、F在同一条直线上，AB=DE，BC=EF，要使△ABC≌△DEF，还需要添加一个条件是（　　）

    A. ∠BCA=∠F B. BC∥EF C. ∠A=∠EDF D. AD=CF

    查看答案和解析>>

    科目：初中数学 来源： 题型：

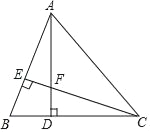
    【题目】如图所示，在△ABC中，AD⊥BC于D，CE⊥AB于E，AD与CE交于点F，且AD=CD．

    （1）求证：△ABD≌△CFD；

    （2）已知BC=7，AD=5，求AF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知∠1和∠2互为补角，∠A=∠D.求证：AB∥CD.

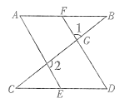
    证明：∵∠1与∠CGD是对顶角，

    ∴∠1=∠CGD（______）.

    又∠1和∠2互为补角（已知），

    ∴∠CGD和∠2互为补角，

    ∴AE∥FD（_________），

    ∴∠A=∠BFD（_______）.

    ∵∠A=∠D(已知），

    ∴∠BFD=∠D（_______），

    AB∥CD（______）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】观察下列图形，寻找对顶角(不含平角)．

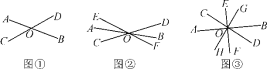
    (1)如图①，图中共有______对对顶角；

    (2)如图②，图中共有______对对顶角；

    (3)如图③，图中共有______对对顶角；

    (4)研究(1)～(3)小题中直线条数与对顶角的对数之间的关系，若有n条直线相交于一点，则可形成__________对对顶角；

    (5)若20条直线相交于一点，则可形成对顶角多少对？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的直径，C为⊙O上一点，PC切⊙O于C，AE⊥PC交PC的延长线于E，AE交⊙O于D，PC与AB的延长线相交于点P，连接AC、BC．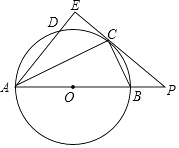

    （1）求证：AC平分∠BAD；
    （2）若PB：PC=1：2，PB=4，求AB的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某次考试中，某班级的数学成绩统计图如图.下列说法错误的是(　　)

    A. 得分在70～80分之间的人数最多 B. 该班的总人数为40

    C. 得分在90～100分之间的人数最少 D. 及格(≥60分)人数是26

    查看答案和解析>>

    同步练习册答案