
【题目】如图,AB是⊙O的直径,C为⊙O上一点,PC切⊙O于C,AE⊥PC交PC的延长线于E,AE交⊙O于D,PC与AB的延长线相交于点P,连接AC、BC.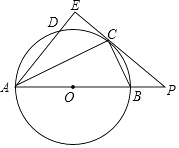
(1)求证:AC平分∠BAD;
(2)若PB:PC=1:2,PB=4,求AB的长.
【答案】
(1)
解:(1)如图所示:连结OC.
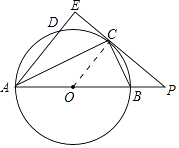
∵PC是⊙O的切线,
∴OC⊥EP.
又∵AE⊥PC,
∴AE∥OC.
∴∠EAC=∠ACO.
又∵∠ACO=∠AOC,
∴∠EAC=∠OAC.
∴AC平分∠BAD;
(2)
解:(2)∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BAC+∠ABC=90°.
∵OB=OC,
∴∠OCB=∠ABC.
∵∠PCB+∠OCB=90°,
∴∠PCB=∠PAC.
∵∠P=∠P,
∴△PCA∽△PBC,
∴ ![]() =
= ![]() ,
,
∴PA= ![]() =16.
=16.
∴AB=PA﹣PB=16﹣4=12.
【解析】(1)先AE∥OC,然后依据平行线的性质可得到∠EAC=∠ACO.,接下来由∠ACO=∠AOC,可证明∠EAC=∠OAC;(2)先证明∠PCB=∠PAC,从而可证明△PCA∽△PBC,依据相似三角形的性质可求得PA的长,最后依据AB=PA﹣PB求解即可.


科目:初中数学 来源: 题型:
【题目】如图,从①∠1=∠2;②∠C=∠D;③∠A=∠F三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( )

A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
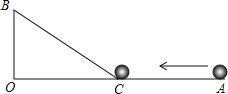
【题目】如图,∠AOB=90°,OA=45cm,OB=15cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
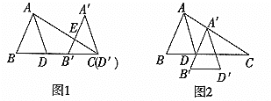
【题目】如图1,平移三角形ABD,使点D沿BD的延长线平移至点C,得到三角形△A'B'D',A'B'交AC于点E,AD平分∠BAC.
(1)猜想∠B'EC与∠A'之间的关系,并写出理由;
(2)如果将三角形ABD平移至如图2所示位置,得到△A'B'D',请问:A'D'平分∠B'A'C吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分别是BG,AC的中点.
(1)求证:DE=DF,DE⊥DF;
(2)连接EF,若AC=10,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
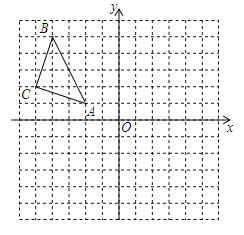
【题目】如图,△ABC在平面直角坐标系中,点A、B、C的坐标分别为A(﹣2,1),B(﹣4,5),C(﹣5,2).
(1)作△ABC关于y对称的△A1B1C1,其中,点A、B、C的对应点分别为A1、B1、C1(不要求写作法);
(2)写出点A1、B1、C1的坐标;
(3)计算△A1B1C1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式,能够表示图中阴影部分的面积的是( )
①ac+(b﹣c)c;②ac+bc﹣c2;③ab﹣(a﹣c)(b﹣c);④(a﹣c)c+(b﹣c)c+c2

A. ①②③④ B. ①②③ C. ①② D. ①
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com