
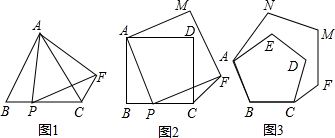
分析 (1)利用△ABC和△APF都是等边三角形,易证△ABP≌△ACF,得出∠ACF=∠B=60°,从而得出∠PCF=120°;
(2)在AB上取BQ=BP,连接QP,易证△AQP≌△PCF,得出∠CFP+∠CPF=∠QAP+∠QPA=45°,即可得出∠PCF=180°-45°=135°,
(3)在AB上取BQ=BP,连接QP,易证△AQP≌△PCF,得出∠CFP+∠CPF=∠QAP+∠QPA=36°,即可得出∠PCF=180°-36°=144°,
(4)同理,在AB上取BQ=BP,连接QP,易证△AQP≌△PCF,得出∠CFP+∠CPF=∠QAP+∠QPA=[180°-$\frac{(n-2)•180°}{n}$]÷2,即可得出∠PCF=180°-[180°-$\frac{(n-2)•180°}{n}$]÷2=90°+$\frac{90°×(n-2)}{n}$.
解答 解:(1)证明:∵△ABC和△APF都是等边三角形,
∴AB=AC,AP=AF,∠BAC=∠PAF=60°,
∴∠BAC-∠PAC=∠PAF-∠PAC,
∴∠BAP=∠CAQF,
在△ABP和△ACQ中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAP=∠CAF}\\{AP=AF}\end{array}\right.$
∴△ABP≌△ACF(SAS),
∴∠ACF=∠B=60°,
∴∠PCF=60°+60°=120°;
(2)如图2,在AB上取BQ=BP,连接QP,∠BQB=45°,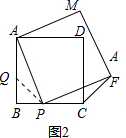
∵∠BAP+∠APB=90°,∠CPF+∠APB=90°,
∴∠BAP=∠CPF,
∵四边形APFM也是正方形,
∴AP=PF,
∵四边形ABCD为正方形,
∴AB=BC,
∴AQ=PC,
在△AQP和△PCF中,
$\left\{\begin{array}{l}{AQ=PC}\\{∠QAP=∠CPF}\\{AP=PF}\end{array}\right.$
∴△AQP≌△PCF(SAS),
∴∠CFP+∠CPF=∠QAP+∠QPA=45°,
∴∠PCF=180°-45°=135°,
(3)如图3,在AB上取BQ=BP,连接QP,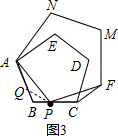
∵五边形ABCDE为正五边形,
∴∠B=108°,
在△AQP和△PCF中,
$\left\{\begin{array}{l}{AQ=PC}\\{∠QAP=∠CPF}\\{AP=PF}\end{array}\right.$
∴△AQP≌△PCF(SAS),
∴∠CFP+∠CPF=∠QAP+∠QPA=36°,
∴∠PCF=180°-36°=144°,
(4)同理可得△AQP≌△PCF(SAS),
∴∠CFP+∠CPF=∠QAP+∠QPA=[180°-$\frac{(n-2)•180°}{n}$]÷2,
∴∠PCF=180°-[180°-$\frac{(n-2)•180°}{n}$]÷2=90°+$\frac{90°×(n-2)}{n}$.
故答案为:90°+$\frac{90°×(n-2)}{n}$.
点评 本题主要考查了全等三角形的判定与性质,涉及正多边形的内角,三角形全等及正多边形的性质,解题的关键是构造全等三角形,利用正多边形的内角求解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
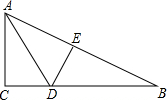 如图,有一块直角三角形纸片,两直角边AC=6,BC=8.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD的长为( )
如图,有一块直角三角形纸片,两直角边AC=6,BC=8.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD的长为( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com