练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】一些完全相同的小正方形搭成一个几何体，这个几何体从正面和左面看所得的平面图形均如图所示，小正方体的块数可能有（ ）

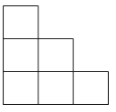
    A. 7种 B. 8种 C. 9种 D. 10种

    【答案】C

    【解析】

    从正面看得到的图形表现了几何体的长与高，从左面看得到的图形表现了几何体的宽和高，得到组合几何体的正方体的最多的个数和最少的个数，进而得到相应的可能情况总数即可．

    解：由2个视图可得该组合几何体有3行，3列，所以最底层最多有9个正方体，最少有3个正方体；第二层最多有4个正方体，最少有2个正方体；第3层最多有1个正方体，最少有1个正方体，所以组合几何体最多有9+4+1=14个正方体，最少有3+2+1=6个正方体．

    故正方体可能的个数在6和14之间，共有9种可能的情况，

    故选C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】下面是小明设计的“过三角形的一个顶点作该顶点对边的平行线”的尺规作图过程．

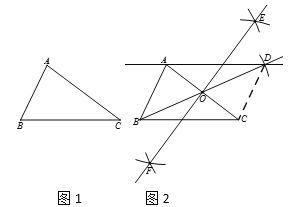
    已知：如图1，△ABC．

    求作：直线AD，使AD∥BC．

    作法：如图2：

    ①分别以点A、C为圆心，以大于AC为半径作弧，两弧交于点E、F；

    ②作直线EF，交AC于点O；

    ③作射线BO，在射线BO上截取OD（B与D不重合），使得OD = OB；

    ④作直线AD．

    ∴ 直线AD就是所求作的平行线．

    根据小明设计的尺规作图过程，完成下面的证明．

    证明：连接CD．

    ∵ＯA =OC，OB=OD，

    ∴四边形ABCD是平行四边形（_______________________）（填推理依据）．

    ∴AD∥BC（__________________________________）（填推理依据）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，△ABC中，∠ABC＝90°，AB＝1，BC＝2，将线段BC绕点C顺时旋转90°得到线段CD，连接AD.

    (1)说明△ACD的形状，并求出△ACD的面积;

    (2)把等腰直角三角板按如图2的方式摆放，顶点E在CB边上，顶点F在DC的延长线上，直角顶点与点C重合.从A，B两题中任选一题作答：

    A .如图3，连接DE，BF,

    ①猜想并证明DE与BF之间的关系；②将三角板绕点C逆时针旋转α(0°＜α＜90°)，直接写出DE与BF之间的关系.

    B .将图2中的三角板绕点C逆时针旋转α(0＜α＜360°)，如图4所示，连接BE，DF，连接点C与BE的中点M,

    ①猜想并证明CM与DF之间的关系；②当CE＝1，CM＝时，请直接写出α的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，圆柱形水管内原有积水的水平面宽CD=20cm，水深GF=2cm．若水面上升2cm（EG=2cm），则此时水面宽

    AB为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，四边形和四边形都是正方形，且，，正方形固定，将正方形绕点顺时针旋转角()．

    （1）如图②，连接、，相交于点，请判断和是否相等？并说明理由；

    （2）如图②，连接，在旋转过程中，当为直角三角形时，请直接写出旋转角的度数；

    （3）如图③，点为边的中点，连接、、，在正方形的旋转过程中，的面积是否存在最大值？若存在，请求出这个最大值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小强骑车从家到学校要经过一段先上坡后下坡的路，在这段路上小强骑车的距离s(千米)与骑车的时间t（分钟）之间的函数关系如图所示，请根据图中信息回答下列问题：

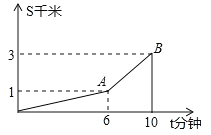
    (1)小强去学校时下坡路长 千米；

    (2)小强下坡的速度为 千米/分钟；

    (3)若小强回家时按原路返回，且上坡的速度不变，下坡的速度也不变，那么回家骑车走这段路的时间是 分钟.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校初二数学兴趣小组活动时，碰到这样一道题：

    “已知正方形AD，点E、F、G、H分别在边AB、BC、CD、DA上，若，则EG=FH”．

    经过思考，大家给出了以下两个方案：

    （甲)过点A作AM∥HF交BC于点M，过点B作BN∥EG交CD于点N；

    （乙)过点A作AM∥HF交BC于点M，作AN∥EG交CD的延长线于点N；

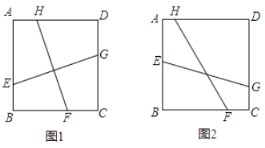
    （1）对小杰遇到的问题，请在甲、乙两个方案中任选一个，加以证明(如图1)

    （2）如果把条件中的“”改为“EG与FH的夹角为45°”，并假设正方形ABCD的边长为1，FH的长为（如图2），试求EG的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我市城建公司新建了一个购物中心，共有商铺30间，据调查分析，当每间的年租金为10万元时，可全部租出：若每间的年租金每增加0.5万元，则少租出商铺一间，为提供优质服务，城建公司引入物业公司代为管理，租出的商铺每间每年需向物业公司缴纳物业费1万元，未租出的商铺不需要向物业公司缴纳物业费．

    （1）当每间商铺的年租金定为13万元时，能租出　 　间．

    （2）当每问商铺的年租金定为多少万元时，该公司的年收益为286万元，且使租客获得实惠？（收益=租金﹣物业费）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC 中，∠BAC＝90°，分别以 AC 和 BC 为边向外作正方形 ACFG 和正方形 BCDE，过点 D 做 FC 的延长线的垂线，垂足为点 H．

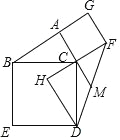
    (1)求证：△ABC≌△HDC；

    (2)连接 FD，交 AC 的延长线于点 M，若 AG＝ ，tan∠ABC＝ ，求△FCM 的面积．

    查看答案和解析>>

    同步练习册答案