
����Ŀ����ͼ���������������Ϊ1�ĵ���ֽ�ϣ��������ڻ��������ڵ�����֮��ľ��붼��1����λ���ȣ����������㶼�ڵ����ϵ������ν������������Σ��밴Ҫ��������в�����

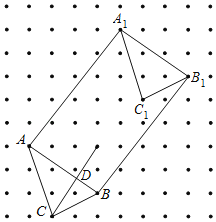
��1����������ABCˮƽ����ƽ��4����λ���ȣ�����ֱ����ƽ��5����λ���ȣ�����ƽ�ƺ����A1B1C1��
��2������AA1��BB1�����߶�AA1��BB1��λ�ù�ϵΪ�� ��������ϵΪ�� �������߶�AA1�ij��ȴ�Լ���� ��AA1���� ��λ���ȣ�����д����������������
��3��������ABC��AB�ϵĸ�CD��
���𰸡���1������������2���߶�AA1�ij��ȴ�Լ��6��AA1��7��λ���ȣ���3����������
��������
��1�����ݡ�ABCˮƽ����ƽ��4����λ���ȣ�����ֱ����ƽ��5����λ���ȣ����ɻ���ƽ�ƺ�ġ�A1B1C1��
��2������ƽ�Ƶ����ʣ����ɵõ��߶�AA1��BB1��λ�ù�ϵ�Լ�������ϵ�����ݹ��ɶ������ɹ����߶�AA1�ij��ȣ�
��3�����ݵ����ABC�������λ�ã���������л����ߵķ��������ɵó���ABC��AB�ϵĸ�CD��
��1����ͼ��ʾ����A1B1C1��Ϊ����
��2����ƽ�Ƶ�����֪���߶�AA1��BB1��λ�ù�ϵΪƽ�У�������ϵΪ��ȣ�
�ɹ��ɶ����ɵã�AA1�ij���Ϊ![]() ��
��
���߶�AA1�ij��ȴ�Լ��6��AA1��7��λ���ȣ�
��3����ͼ��ʾ��CD��Ϊ����


 ���100��1�ž�ϵ�д�
���100��1�ž�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���֪A��a��b������a.b����![]() ��
��
��1����A������꼰�߶�OA�ij��ȣ���2����PΪx����������һ�㣬�ҡ�AOP�ǵ��������Σ���P������ꣻ
��3����ͼ2����B��1��0����C��0����3������ȷ����ACO+��BCO��ֵ�Ƿ����仯�������䣬����ֵ�����仯��������仯��Χ��


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����![]() �У�AB=AC����ABC =
�У�AB=AC����ABC =![]() ��D��BC����һ�㣬��ADΪ����
��D��BC����һ�㣬��ADΪ����![]() ��ʹAE=AD��
��ʹAE=AD��![]() +
+![]() =180����
=180����
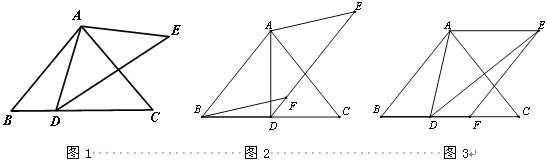
��1��ֱ��д����ADE�Ķ������ú�![]() ��ʽ�ӱ�ʾ����
��ʽ�ӱ�ʾ����
��2����AB��AEΪ����ƽ���ı���ABFE��
����ͼ2������Fǡ������DE�ϣ���֤��BD=CD��
����ͼ3������Fǡ������BC�ϣ���֤��BD=CF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ����ͬѧ�Ǿ�Уѧ����ε�У���������һ�ε��飬�����������Ƴ�������ͼ������ͳ��ͼ���������ͼ����Ϣ������и��⣺

��1���˴ι�������___________λѧ��.
��2���뽫����ͳ��ͼ��������.
��3�����ѧУ��1000��ѧ���������������������ж��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
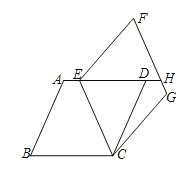
����Ŀ����ͼ����ȫ��ͬ����������ABCD��ECGF�Ķ���C�غϣ���B=��F����Eǡ���ڱ�AD�ϣ��ӳ�ED��FG�ڵ�H��
��1����֤����B=��ECB��
��2������BE��CH��
�����ж��ı���BEHC����״����˵�����ɣ�
����֤��CHƽ����DCG��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ֱ��AD��EF����B��C�ֱ���EF��AD�ϣ���A=��ABC��BDƽ����CBF��
��1����֤��AB��BD��
��2����ͼ2��BG��AD�ڵ�G����֤����ACB=2��ABG��
��3���ڣ�2���������£���ͼ3��CHƽ����ACB��BG�ڵ�H������ABG=������ֱ��д����BHC�Ķ��������ú�����ʽ�ӱ�ʾ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��С��Ʒ�ijɱ���Ϊ10Ԫ/kg���г����鷢�֣��ò�Ʒÿ���������w��kg�������ۼ�x��Ԫ/kg�������¹�ϵw=��2x+100�������ֲ�Ʒÿ�����������Ϊy��Ԫ����
��1����y��x֮��ĺ�����ϵʽ��
��2�����ۼ۶�Ϊ����Ԫʱ��ÿ����������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ����ȫ��ѧ����������д��������ÿλѧ����д����39���������ȡ�˲���ѧ������д��������Ƴ����µ�ͼ��,���������Ϣ����������⣺
��1��ͳ�Ʊ��е�![]() ��
��![]() ��
��
��2������ͳ��ͼ�С�C�顱����Ӧ��Բ�ĽǵĶ����� ��
��3����֪��У����900��ѧ���������д��ȷ���ֵĸ�������24����Ϊ���ϸ�������Ƹ�У������д�������ϸ��ѧ��������

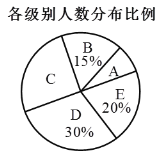
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com