
【题目】如图,在△ABC中,AB=AC=5,![]() ,将△ABC绕点B逆时针旋转,得到
,将△ABC绕点B逆时针旋转,得到![]() ,当点
,当点![]() 在线段CA延长线上时
在线段CA延长线上时![]() 的面积为_________.
的面积为_________.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
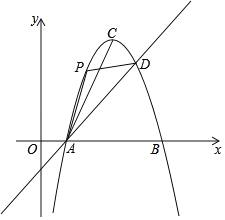
【题目】如图,直线y=x﹣1与抛物线y=﹣x2+6x﹣5相交于A、D两点.抛物线的顶点为C,连结AC.
(1)求A,D两点的坐标;
(2)点P为该抛物线上一动点(与点A、D不重合),连接PA、PD.
①当点P的横坐标为2时,求△PAD的面积;
②当∠PDA=∠CAD时,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,点
两点,点![]() 在点
在点![]() 的左侧,抛物线与
的左侧,抛物线与![]() 轴正半轴交于点
轴正半轴交于点![]() ,分别连接
,分别连接![]() 、
、![]() ,则有
,则有![]() ,
,![]() ,
,
(1)求抛物线的函数表达式;
(2)设![]() 为抛物线的顶点,点
为抛物线的顶点,点![]() 为线段
为线段![]() 上任意一点,过点
上任意一点,过点![]() 作
作![]() 轴的垂线分别交直线
轴的垂线分别交直线![]() 及抛物线于点
及抛物线于点![]() 、点
、点![]() ,当
,当![]() 是锐角三角形时,求
是锐角三角形时,求![]() 的取值范围.
的取值范围.
(3)在(2)的前提下,设![]() ,求
,求 ![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:
在综合与实践课上,老师让同学们以“矩形纸片的剪拼”为主题开展数学活动.如图1,将:矩形纸片ABCD沿对角线AC剪开,得到△ABC和△ACD.并且量得AB=2cm,AC=4cm.
操作发现:
(1)将图1中的△ACD以点A为旋转中心,按逆时针方向旋转![]() ,使
,使![]() ,得到如图2所示的△
,得到如图2所示的△![]() ,过点C作
,过点C作![]() 的平行线,与
的平行线,与![]() 的延长线交于点E,则四边形
的延长线交于点E,则四边形![]() 的形状是 .
的形状是 .
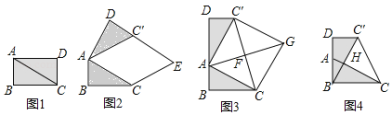
(2)创新小组将图1中的△ACD以点A为旋转中心,按逆时针方向旋转,使B、A、D三点在同一条直线上,得到如图3所示的△![]() ,连接
,连接![]() ,取
,取![]() 的中点F,连接AF并延长至点G,使FG=AF,连接CG、
的中点F,连接AF并延长至点G,使FG=AF,连接CG、![]() ,得到四边形
,得到四边形![]() ,发现它是正方形,请你证明这个结论.
,发现它是正方形,请你证明这个结论.
实践探究:
(3)缜密小组在创新小组发现结论的基础上,进行如下操作:将△ABC沿着BD方向平移,使点B与点A重合,此时A点平移至![]() 点,
点,![]() 与
与![]() 相交于点H,如图4所示,连接
相交于点H,如图4所示,连接![]() ,试求
,试求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】参照学习函数的过程与方法,探究函数y=![]() 的图象与性质.
的图象与性质.
因为y=![]() ,即y=﹣
,即y=﹣![]() +1,所以我们对比函数y=﹣
+1,所以我们对比函数y=﹣![]() 来探究.
来探究.
列表:
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | ﹣ |
| 1 | 2 | 3 | 4 | … |
y=﹣ | … |
|
| 1 | 2 | 4 | ﹣4 | ﹣1 | 1 | ﹣ | ﹣ | … |
y= | … |
|
| 2 | 3 | 5 | ﹣3 | ﹣1 | 0 |
|
| … |
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以y=![]() 相应的函数值为纵坐标,描出相应的点,如图所示:
相应的函数值为纵坐标,描出相应的点,如图所示:
(1)请把y轴左边各点和右边各点,分别用一条光滑曲线顺次连接起来;
(2)观察图象并分析表格,回答下列问题:
①当x<0时,y随x的增大而 ;(填“增大”或“减小”)
②y=![]() 的图象是由y=﹣
的图象是由y=﹣![]() 的图象向 平移 个单位而得到;
的图象向 平移 个单位而得到;
③图象关于点 中心对称.(填点的坐标)
(3)设A(x1,y1),B(x2,y2)是函数y=![]() 的图象上的两点,且x1+x2=0,试求y1+y2+3的值.
的图象上的两点,且x1+x2=0,试求y1+y2+3的值.
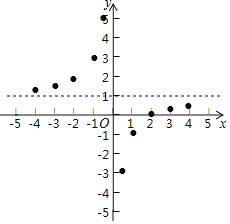
查看答案和解析>>
科目:初中数学 来源: 题型:
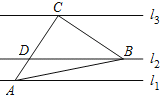
【题目】如图,直线![]() ∥
∥![]() ∥
∥![]() ,一等腰Rt△ABC的三个顶点A、B、C分别在直线
,一等腰Rt△ABC的三个顶点A、B、C分别在直线![]() 、
、![]() 、
、![]() 上,∠ACB=90°,AC交
上,∠ACB=90°,AC交![]() 于点D.若
于点D.若![]() 与
与![]() 的距离为1,
的距离为1,![]() 与
与![]() 的距离为4,则
的距离为4,则![]() 的值是( )
的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技的进步和网络资源的丰富,在线学习已成为更多人的自主学习选择,某校计划为学生提供以下四类在线学习方式:在线阅读、在线听课、在线答题和在线讨论,为了解学生需求,该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据调查结果绘制成如下两幅不完整的统计图.
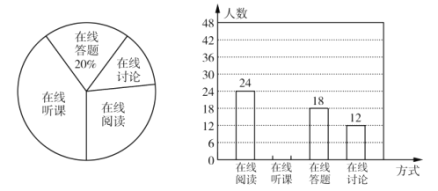
根据图中信息,解答下列问题:
(1)求本次调查的学生总人数,并通过计算补全条形统计图;
(2)求扇形统计图中“在线讨论”对应的扇形圆心角的度数;
(3)该校共有学生1800人,请你估计该校对在线阅读最感兴趣的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于A,B(﹣1,0)两点,与y轴交于点C,则下列四个结论:①ac<0;②2a+b=0;③﹣1<x<3时,y<0;④4a+c<0.其中所有正确结论的序号是( )
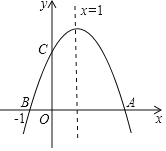
A.①②④B.①③④C.①②③D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 的二次函数
的二次函数![]() 的图象开口向下,
的图象开口向下,![]() 与
与![]() 的部分对应值如下表所示:
的部分对应值如下表所示:
|
|
|
|
|
|
|
|
|
|
|
|
下列判断,①![]() ;②
;②![]() ;③方程
;③方程![]() 有两个不相等的实数根;
有两个不相等的实数根;
④若![]() ,则
,则![]() ,正确的是________________(填写正确答案的序号) .
,正确的是________________(填写正确答案的序号) .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com