
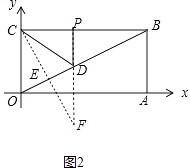
【题目】如图,在平面直角坐标系中,四边形OABC是矩形,其中点A在x轴的正半轴上,点B的坐标为(4,2),点D为对角线OB上一个动点(不包括端点),∠BCD的平分线交OB于点E.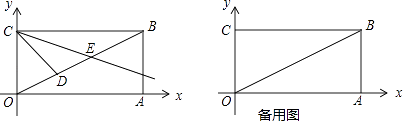
(1)求线段OB所在直线的函数表达式,并写出CD的取值范围.
(2)当∠BCD的平分线经过点A时,求点D的坐标.
(3)点P是线段BC上的一个动点,求CD十DP的最小值.
【答案】
(1)
解:设线段OB所在直线的函数表达式为y=kx,
把B(4,2)代入,得2=4k,解得k= ![]() ,
,
∴线段OB所在直线的函数表达式为y= ![]() x.
x.
CD的范围: ![]() ≤CD<4
≤CD<4
(2)
解:如图1中,延长CD交OA于点F,
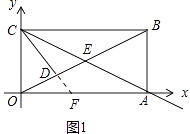
∵∠ACF=∠ACB=∠CAF,
∴AF=CF,设AF=CF=m,则OF=4﹣m,
∵OF2+OC2=CF2,
∴(4﹣m)2+22=m2,解得m= ![]() ,
,
∴直线CF的解析式为y=﹣ ![]() x+2,
x+2,
由 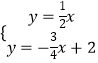 解得
解得 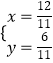 ,
,
∴点D坐标( ![]() ,
, ![]() )
)
(3)
解:如图2中,作点C关于直线OB的对称点F,作FP⊥BC,交OB于D,垂足为P,则点P、D就是所求的点,此时DC+DP=DF+PD=FP最短(垂线段最短).
设直线CF的解析式为y=﹣2x+b,把C(0,2)代入得b=2,
∴直线CF解析式为y=﹣2x+2,设直线CF交OB于点E,
由 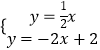 解得
解得 ![]() ,
,
∴点E坐标( ![]() ,
, ![]() ),
),
∵C、F关于点E对称,
∴点F坐标( ![]() ,﹣
,﹣ ![]() ),
),
∴CD+PD最小值=PF=2+ ![]() =
= ![]()
【解析】(1)设线段OB所在直线的函数表达式为y=kx,把B(4,2)代入求出k即可解决问题.(2)如图1中,延长CD交OA于点F,设AF=CF=m,则OF=4﹣m,由OF2+OC2=CF2 , 列出方程求出m,求出直线CF的解析式,解方程组即可解决问题.(3)如图2中,作点C关于直线OB的对称点F,作FP⊥BC,交OB于D,垂足为P,则点P、D就是所求的点,此时DC+DP=DF+PD=FP最短,求出点F坐标即可解决问题.
【考点精析】解答此题的关键在于理解正比例函数的图象和性质的相关知识,掌握正比函数图直线,经过一定过原点.K正一三负二四,变化趋势记心间.K正左低右边高,同大同小向爬山.K负左高右边低,一大另小下山峦,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB⊥BD, ![]() =
= ![]() ,将ABCD放置在平面直角坐标系中,且AD⊥x轴,点D的横坐标为1,点C的纵坐标为3,恰有一条双曲线
,将ABCD放置在平面直角坐标系中,且AD⊥x轴,点D的横坐标为1,点C的纵坐标为3,恰有一条双曲线 ![]() (k>0)同时经过B、D两点,则点B的坐标是
(k>0)同时经过B、D两点,则点B的坐标是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,AB=3cm,AD=6cm,∠ADC的角平分线DE交BC于点E,交AC于点F,CG⊥DE,垂足为G,DG= ![]() cm,则EF的长为( )
cm,则EF的长为( ) 
A.2cm
B.![]() cm
cm
C.1cm
D.![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(1,1),B(4,0),C(4,4). 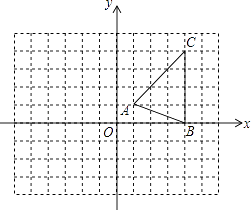
(1)按下列要求作图:
①将△ABC向左平移4个单位,得到△A1B1C1;
②将△A1B1C1绕点B1逆时针旋转90°,得到△A2B2C2 .
(2)求点C1在旋转过程中所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织了一次初三科技小制作比赛,有A、B、C、D四个班共提供了100件参赛作品,C班提供的参赛作品的获奖率为50%,其他几个班的参赛作品情况及获奖情况绘制在下列图1和图2两幅尚不完整的统计图中. 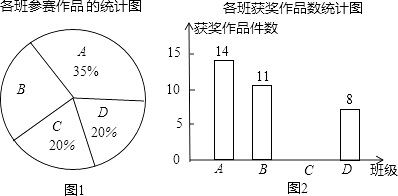
(1)B班参赛作品有多少件?
(2)请你将图2的统计图补充完整;
(3)通过计算说明,哪个班的获奖率高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在坡角为30°的山坡上有一铁塔AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得铁塔AB落在斜坡上的影子BD的长为6米,落在广告牌上的影子CD的长为4米,求铁塔AB的高(AB,CD均与水平面垂直,结果保留根号). 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC内接于⊙O,∠BAC的平分线AD交⊙O于点D,交BC于点E,过点D作DF∥BC,交AB的延长线于点F. 
(1)求证:△BDE∽∠ADB;
(2)试判断直线DF与⊙O的位置关系,并说明理由;
(3)如图2,条件不变,若BC恰好是⊙O的直径,且AB=6,AC=8,求DF的长. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
如果函数y=f(x)满足:对于自变量x的取值范围内的任意x1 , x2 ,
① 若x1<x2 , 都有f(x1)<f(x2),则称f(x)是增函数;
②若x1<x2 , 都有f(x1)>f(x2),则称f(x)是减函数.
例题:证明函数f(x)= ![]() (x>0)是减函数.
(x>0)是减函数.
证明:假设x1<x2 , 且x1>0,x2>0
f(x1)﹣f(x2)= ![]() ﹣
﹣ ![]() =
= ![]() =
= ![]()
∵x1<x2 , 且x1>0,x2>0
∴x2﹣x1>0,x1x2>0
∴ ![]() >0,即f(x1)﹣f(x2)>0
>0,即f(x1)﹣f(x2)>0
∴f(x1)>f(x2)
∴函数f(x)= ![]() (x>0)是减函数.
(x>0)是减函数.
根据以上材料,解答下面的问题:
(1)函数f(x)= ![]() (x>0),f(1)=
(x>0),f(1)= ![]() =1,f(2)=
=1,f(2)= ![]() =
= ![]() .
.
计算:f(3)= , f(4)= , 猜想f(x)= ![]() (x>0)是函数(填“增”或“减”);
(x>0)是函数(填“增”或“减”);
(2)请仿照材料中的例题证明你的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com