
(本题10分)如图,在Rt△ABC中,∠C=90°,点P为AC边上的一点,将线段AP绕点A顺时针方向旋转(点P对应点P′),当AP旋转至AP′⊥AB时,点B、P、P′恰好在同一直线上,此时作P′E⊥AC于点E.

(1)求证:∠CBP=∠ABP;
(2)求证:AE=CP;
(3)当 ,BP′=
,BP′= 时,求线段AB的长.
时,求线段AB的长.
(1)证明见试题解析;(2)证明见试题解析;(3)10.
【解析】
试题分析:(1)根据旋转的性质可得AP=AP′,根据等边对等角的性质可得∠APP′=∠AP′P,再根据等角的余角相等证明即可;
(2)过点P作PD⊥AB于D,根据角平分线上的点到角的两边的距离相等可得CP=DP,然后求出∠PAD=∠AP′E,利用“角角边”证明△APD和△P′AE全等,根据全等三角形对应边相等可得AE=DP,从而得证;
(3)设CP=3k,PE=2k,表示出AE=CP=3k,AP′=AP=5k,然后利用勾股定理列式求出P′E=4k,再求出△ABP′和△EPP′相似,根据相似三角形对应边成比例列式求出P′A= AB,然后在Rt△ABP′中,利用勾股定理列式求解即可.
AB,然后在Rt△ABP′中,利用勾股定理列式求解即可.
试题解析:∵AP′是AP旋转得到,∴AP=AP′,∴∠APP′=∠AP′P,
∵∠C=90°,AP′⊥AB,∴∠CBP+∠BPC=90°,∠ABP+∠AP′P=90°,
又∵∠BPC=∠APP′(对顶角相等),∴∠CBP=∠ABP;
(2)证明:如图,过点P作PD⊥AB于D,
∵∠CBP=∠ABP,∠C=90°,∴CP=DP,
∵P′E⊥AC,∴∠EAP′+∠AP′E=90°,
又∵∠PAD+∠EAP′=90°,∴∠PAD=∠AP′E,
在△APD和△P′AE中,∵∠PAD=∠AP′E,∠ADP=∠P′EA=90°,AP=AP′,∴△APD≌△P′AE(AAS),∴AE=DP,∴AE=CP;
(3)解:∵ ,∴设CP=3k,PE=2k,则AE=CP=3k,AP′=AP=3k+2k=5k,
,∴设CP=3k,PE=2k,则AE=CP=3k,AP′=AP=3k+2k=5k,
在Rt△AEP′中,P′E= ,
,
∵∠C=90°,P′E⊥AC,∴∠CBP+∠BPC=90°,∠EP′P+∠P′PE=90°,
∵∠BPC=∠EPP′(对顶角相等),∴∠CBP=∠P′PE,
又∵∠BAP′=∠P′EP=90°,∴△ABP′∽△EPP′,∴AB:P′E=P′A:PE,即AB:4k=P′A:2k,
解得P′A= AB,
AB,
在Rt△ABP′中, ,即
,即 ,解得AB=10.
,解得AB=10.

考点:1.全等三角形的判定与性质;2.角平分线的性质;3.相似三角形的判定与性质.


 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源:2014-2015学年江苏省江阴市要塞片九年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,在△ABC中,C=  ,BC=6,AC=8,则△ABC内切圆的半径是 。
,BC=6,AC=8,则△ABC内切圆的半径是 。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市要塞片七年级上学期期中考试数学试卷(解析版) 题型:选择题
在数-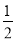 ,-|-2|,+[-(-2)], (-2)3,中负数的个数是 ( )
,-|-2|,+[-(-2)], (-2)3,中负数的个数是 ( )
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市八年级上学期期中考试数学试卷(解析版) 题型:选择题
实数
 ,
,
 ,
, ,
, ,0.1010010001,其中是无理数的有( )
,0.1010010001,其中是无理数的有( )
A.2个 B.3个 C.4个 D.5个
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市八年级上学期期中考试数学试卷(解析版) 题型:解答题
已知直线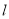 及其两侧两点A、B,如图.
及其两侧两点A、B,如图.
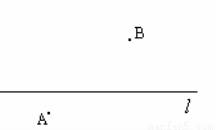
(1)在直线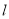 上求一点P,使PA=PB;
上求一点P,使PA=PB;
(2)在直线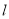 上求一点Q,使
上求一点Q,使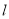 平分∠AQB. (以上两小题保留作图痕迹,标出必要的字母,不要求写作法.)
平分∠AQB. (以上两小题保留作图痕迹,标出必要的字母,不要求写作法.)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市九年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,在 中,
中, ,
, .动点
.动点 分别在直线
分别在直线 上运动,且始终保持
上运动,且始终保持 .设
.设 ,
, ,则
,则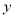 与
与 之间的函数关系用图象大致可表示为 ( )
之间的函数关系用图象大致可表示为 ( )


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com