
【题目】为了了解某区九年级数学教学质量检测情况,进行了抽样调查,其过程如下,请补全表一、表二中的空白,并回答提出的问题.
收集数据:随机抽取甲、乙两所学校中各自取20名学生的数学成绩进行分析
甲:91 89 77 86 71 31 97 93 72 91 81 92 85 85 95 88 88 90 44 91
乙:84 93 66 69 76 87 77 82 85 88 90 88 67 88 91 96 68 97 59 88
整理数据:表一
分段 学校 | 30≤x≤39 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 1 | 1 | 0 | 0 | 3 | 7 | 8 |
乙 | 0 | 0 | 1 | 2 | 8 | 5 |
分析数据:表二
统计量 学校 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 81.85 | 88 | 91 | 268.43 |
乙 | 81.95 | 86 | 115.25 |
得出结论:
(1)若甲学校有400名九年级学生,估计这次考试成绩80分(包含80分)以上人数为 .
(2)可以推断出 (填:甲或乙)学校学生的数学水平较高,理由是 (至少从两个不同角度说明推断的合理性).
【答案】(1)300;(2)答案不唯一,理由见解析
【解析】
依据统计表中的数据,即可得到乙校各分数段的人数,以及众数的大小;依据甲学校考试成绩80分以上人数所占的百分比,即可得到有400名初二学生中这次考试成绩80分以上人数;从平均数、中位数以及众数的角度分析,即可得到哪个学校学生的数学水平较高.
解:表一
学校 | 30≤x≤39 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 1 | 1 | 0 | 0 | 3 | 7 | 8 |
乙 | 0 | 0 | 1 | 4 | 2 | 8 | 5 |
统计量
表二
学校 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 81.85 | 88 | 91 | 268.43 |
乙 | 81.95 | 86 | 88 | 115.25 |
(1)若甲学校有400名初二学生,估计这次考试成绩80分以上人数为![]() .
.
故答案为:300;
(2)(答案不唯一)
选择甲,其理由是两校平均数基本相同,而甲校的中位数以及众数均高于乙校,说明甲校学生的数学水平较高.
选择乙,其理由是乙校的平均数较高于甲校的平均数,方差低于甲校,说明乙校学生的数学成绩波动比甲校要小,总体成绩稳定,最高与最低相差不大,再根据平均数,可以判断总体水平较高.


科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 为
为![]() 上一点,点
上一点,点![]() 是半径
是半径![]() 上一动点(不与
上一动点(不与![]() ,
,![]() 重合),过点
重合),过点![]() 作射线
作射线![]() ,分别交弦
,分别交弦![]() ,
,![]() 于
于![]() ,
,![]() 两点,在射线
两点,在射线![]() 上取点
上取点![]() ,使
,使![]() .
.

(1)求证:![]() 是
是![]() 的切线.
的切线.
(2)当![]() 是
是![]() 的中点时;
的中点时;
①若![]() ,求证:以
,求证:以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是菱形;
为顶点的四边形是菱形;
②若![]() ,且
,且![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() (k≠8)的图像经过点A(1,6).
(k≠8)的图像经过点A(1,6).
(1)求k的值;
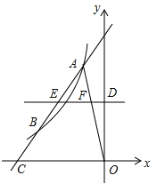
(2)如图,过点A作直线AC与函数![]() 的图像交于点B,与x轴交于点C,且AB=2BC,求直线AC的解析式;
的图像交于点B,与x轴交于点C,且AB=2BC,求直线AC的解析式;
(3)在(2)的条件下,连接OA,过y轴的正半轴上的一点D作直线DE∥x轴,分别交线段AC、OA于点E、F,若△AEF的面积为![]() ,求点D的坐标.
,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过
经过![]() ,
,![]() 两点,与
两点,与![]() 轴正半轴交于点
轴正半轴交于点![]() .
.
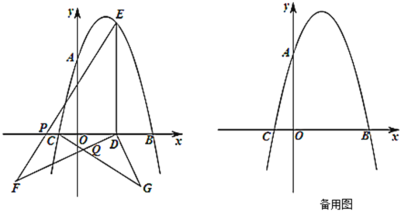
(1)求抛物线的解析式;
(2)![]() 为线段
为线段![]() 上一点,过
上一点,过![]() 作
作![]() 轴的垂线,交抛物线于点
轴的垂线,交抛物线于点![]() ,将线段
,将线段![]() ,
,![]() 绕点
绕点![]() 逆时针旋转任意相同的角到
逆时针旋转任意相同的角到![]() ,
,![]() 的位置,使点
的位置,使点![]() ,
,![]() 的对应点
的对应点![]() ,
,![]() 都在
都在![]() 轴下方,
轴下方,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() .当
.当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)![]() 在抛物线上,
在抛物线上,![]() 在坐标平面内,当以
在坐标平面内,当以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为矩形时,直接写出点
为顶点的四边形为矩形时,直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
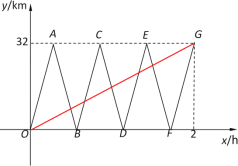
【题目】某观光湖风景区,一观光轮与一巡逻艇同时从甲码头出发驶往乙码头,巡逻艇匀速往返于甲、乙两个码头之间,当观光轮到达乙码头时,巡逻艇也同时到达乙码头.设出发x h后,观光轮、巡逻艇离甲码头的距离分别为y1 km、y2 km.图中的线段OG、折线OABCDEFG分别表示y1、y2 与x之间的函数关系.
(1)观光轮的速度是 km/h,巡逻艇的速度是 km/h;
(2)求整个过程中观光轮与巡逻艇的最大距离;
(3)求整个过程中观光轮与巡逻艇相遇的最短时间间隔.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的三角形,如图所示,已知∠A=90°, BD=4,CF=6, 则AO的长是 ( )

A.![]() B.
B.![]() C.
C.![]() D.4
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
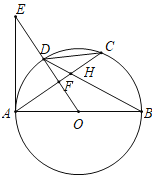
【题目】如图,AB是![]() 的直径,C是
的直径,C是![]() 上一点,D是
上一点,D是![]() 的中点,
的中点,![]() 为
为![]() 延长线上一点,AE切
延长线上一点,AE切![]() 于A,AC与BD交于点H,与OE交于点F,连结EC.
于A,AC与BD交于点H,与OE交于点F,连结EC.
(1)求证:EC是![]() 的切线;
的切线;
(2)若DH=9,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
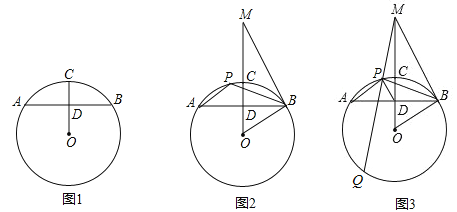
【题目】(2017黑龙江省哈尔滨市,第26题,10分)已知:AB是⊙O的弦,点C是![]() 的中点,连接OB、OC,OC交AB于点D.
的中点,连接OB、OC,OC交AB于点D.
(1)如图1,求证:AD=BD;
(2)如图2,过点B作⊙O的切线交OC的延长线于点M,点P是![]() 上一点,连接AP、BP,求证:∠APB﹣∠OMB=90°;
上一点,连接AP、BP,求证:∠APB﹣∠OMB=90°;
(3)如图3,在(2)的条件下,连接DP、MP,延长MP交⊙O于点Q,若MQ=6DP,sin∠ABO=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市用3 000元购进某种干果销售,由于销售状况良好,超市又调拨9 000元购进该种干果,但这次的进价比第一次的进价提高了20%,购进干果数量比第一次的2倍还多300 kg.如果超市按9元/kg的价格出售,当大部分干果售出后,余下的600 kg按售价的八折售完.
(1)该种干果第一次的进价是多少?
(2)超市销售这种干果共盈利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com