
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 为
为![]() 上一点,点
上一点,点![]() 是半径
是半径![]() 上一动点(不与
上一动点(不与![]() ,
,![]() 重合),过点
重合),过点![]() 作射线
作射线![]() ,分别交弦
,分别交弦![]() ,
,![]() 于
于![]() ,
,![]() 两点,在射线
两点,在射线![]() 上取点
上取点![]() ,使
,使![]() .
.

(1)求证:![]() 是
是![]() 的切线.
的切线.
(2)当![]() 是
是![]() 的中点时;
的中点时;
①若![]() ,求证:以
,求证:以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是菱形;
为顶点的四边形是菱形;
②若![]() ,且
,且![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)①见解析,②5
【解析】
(1)如图1,连接OC.则OC=OB,根据等腰三角形的性质等边对等角可得:∠OBC=∠OCB.再由垂直的定义可得∠BPD=90°.又根据三角形的内角和定理可得∠OBC+∠BDP=90°.由FC=FD可得∠FCD=∠FDC.又因为∠FDC=∠BDP,所以
∠OCB+∠FCD=90°,从而可证明.
(2)①如图2,连接OE,BE,CE.先由已知条件证出△BOE,△OCE均为等边三角形,再根据等边三角形的三条边相等可证得:OB=BE=CE=OC,从而根据四条边相等的四边形是菱形可证得结果.
②构造直角三角形,利用三角函数和勾股定理求即可.
(1)证明:如图1,连接OC.
∵OB=OC,∴∠OBC=∠OCB.
∵PF⊥AB,∴∠BPD=90°.∴∠OBC+∠BDP=90°.
∵FC=FD,∴∠FCD=∠FDC.
又∵∠FDC=∠BDP,
∴∠OCB+∠FCD=90°,即∠OCF=90°.
∴FC是⊙O的切线.
图1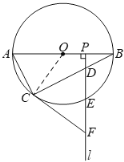
(2)①证明:如图2,连接OE,BE,CE.
∵AB是⊙O的直径,∴∠ACB=90°.
∵∠BAC=60°,∴∠BOC=2∠BAC=120°.
∵E是![]() 的中点,即
的中点,即![]() ,
,
∴∠BOE=∠COE=60°.
又∵OB=OE=OC,∴△BOE,△OCE均为等边三角形.
∴OB=BE=CE=OC.∴四边形BOCE是菱形.
②解:如图2,记OE与BC的交点为H.
∵AB是⊙O的直径,∴∠ACB=90°.
∴在Rt△ABC中,tan∠ABC=![]() =
=![]() .
.
设AC=3k,BC=4k(k>0).
∵AC2+BC2=AB2,
∴(3k)2+(4k)2=202,解得k=4.
∴AC=12,BC=16.
∵E是![]() 的中点,OE是⊙O的半径,
的中点,OE是⊙O的半径,
∴OE⊥BC,BH=CH=![]() BC=8.
BC=8.
∵S△BOE=![]() OE·BH=
OE·BH=![]() OB·PE,OE=OB=
OB·PE,OE=OB=![]() AB=10,
AB=10,
∴PE=![]() =
=![]() =8.
=8.
在Rt△OPE中,OP=![]() =
=![]() =6.
=6.
∴BP=OB-OP=10-6=4.
在Rt△BPD中,![]() =tan∠ABC=
=tan∠ABC=![]() ,∴DP=
,∴DP=![]() BP=
BP=![]() ×4=3.
×4=3.
∴DE=PE-DP=8-3=5.
图2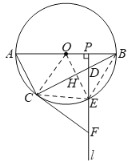
【点晴】
本题是圆的综合题,难度较大,灵活运用知识作出合理的辅助线构造直角三角形是解题的关键.


科目:初中数学 来源: 题型:
【题目】![]() 年中国“两会时间”
年中国“两会时间”![]() 月
月![]() 日正式开启,特殊时期召开的中国两会备受世界瞩目.某校为让学生进一步了解
日正式开启,特殊时期召开的中国两会备受世界瞩目.某校为让学生进一步了解![]() 年“两会”热点,计划开展关于两会的宣讲活动,开展活动之前,教务处随机抽取若干名学生,对“你最想听的宣讲内容”进行了调查,有
年“两会”热点,计划开展关于两会的宣讲活动,开展活动之前,教务处随机抽取若干名学生,对“你最想听的宣讲内容”进行了调查,有![]() .民生改善、
.民生改善、![]() .国家治理、
.国家治理、![]() .生态文明建设、
.生态文明建设、![]() .法治保障四项宣讲内容,经统计,被调查学生按学校要求,并结合自身的兴趣,每人从这四项宣讲内容中选择一项现将调查结果绘制成如下两幅不完整的统计图.
.法治保障四项宣讲内容,经统计,被调查学生按学校要求,并结合自身的兴趣,每人从这四项宣讲内容中选择一项现将调查结果绘制成如下两幅不完整的统计图.
结合图中信息解答下列问题:
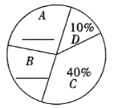
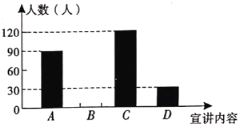
(1)请将两幅统计图补充完整,所抽取学生最想听的宣讲内容的众数是_____;
(2)在这次调查中,哪项宣讲内容的选择人数少于各项宣讲内容选择人数的平均数?
(3)若本校一共有![]() 名学生,请估计“最想听国家治理”的人数.
名学生,请估计“最想听国家治理”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情初期,某市出台《中小学教师志愿辅导工作实施意见》,鼓励教师参与志愿辅导,该市率先示范,推出名师公益课程,为学生提供线上免费辅导,据统计,第一批公益课受益学生![]() 万人次,第三批公益课受益人数
万人次,第三批公益课受益人数![]() 万人次.
万人次.
(1)如果第二批,第三批公益课受益学生人次的增长率相同,求这个增长率;
(2)按照这个增长率,预计第四批公益课受益学生将达到多少万人次?
查看答案和解析>>
科目:初中数学 来源: 题型:
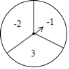
【题目】如图,可以自由转动的转盘被平均分成了三等分标有数字﹣2,3,﹣1的扇形区域转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止)
(1)转动转盘一次,求转出的数字是3的概率;
(2)转动转盘两次,设第一次得到的数字为x,第二次得到的数字为y,点M的坐标为(x,y),请用树状图或列表法求点M在反比例函数y=﹣![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂准备今年春季开工前美化厂区,计划对面积为![]() 的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为
的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为![]() 区域的绿化时,甲队比乙队少用6天.
区域的绿化时,甲队比乙队少用6天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少![]() ?
?
(2)若工厂每天需付给甲队的绿化费用为0.4万元,乙队为0.5万元,要使这次的绿化总费用不超过10万元,至少应安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第5代移动通信技术简称5G,某地已开通5G业务,经测试5G下载速度是4G下载速度的15倍,小明和小强分别用5G与4G下载一部600兆的公益片,小明比小强所用的时间快140秒,求该地4G与5G的下载速度分别是每秒多少兆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=6,DC=2,点P是AB上的动点,则PC+PD的最小值为( )

A.8B.10C.12D.14
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某区九年级数学教学质量检测情况,进行了抽样调查,其过程如下,请补全表一、表二中的空白,并回答提出的问题.
收集数据:随机抽取甲、乙两所学校中各自取20名学生的数学成绩进行分析
甲:91 89 77 86 71 31 97 93 72 91 81 92 85 85 95 88 88 90 44 91
乙:84 93 66 69 76 87 77 82 85 88 90 88 67 88 91 96 68 97 59 88
整理数据:表一
分段 学校 | 30≤x≤39 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 1 | 1 | 0 | 0 | 3 | 7 | 8 |
乙 | 0 | 0 | 1 | 2 | 8 | 5 |
分析数据:表二
统计量 学校 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 81.85 | 88 | 91 | 268.43 |
乙 | 81.95 | 86 | 115.25 |
得出结论:
(1)若甲学校有400名九年级学生,估计这次考试成绩80分(包含80分)以上人数为 .
(2)可以推断出 (填:甲或乙)学校学生的数学水平较高,理由是 (至少从两个不同角度说明推断的合理性).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com