
【题目】如图,在平面直角坐标系中,一次函数y=ax+b的图象与反比例函数y=![]() 的图象交于一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,m),点B的坐标为(n,﹣2),tan∠BOC=
的图象交于一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,m),点B的坐标为(n,﹣2),tan∠BOC=![]() .
.
(1)求该反比例函数和一次函数的解析式.
(2)求△BOC的面积.
(3)P是x轴上的点,且△PAC的面积与△BOC的面积相等,求P点的坐标.
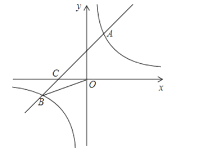
【答案】(1)反比例函数为y=![]() ,一次函数的解析式为:y=x+2;(2)2;(3)P(-3,0)或P(-1,0).
,一次函数的解析式为:y=x+2;(2)2;(3)P(-3,0)或P(-1,0).
【解析】
试题(1)过B作x轴的垂线,垂足为D,求出BD=2,根据tan∠BOC=![]() 求出OD=4,得出B的坐标,把B的坐标代入y=
求出OD=4,得出B的坐标,把B的坐标代入y=![]() 即可求出反比例函数的解析式,求出A的坐标,把A、B的坐标代入一次函数的解析式,即可求出解析式;
即可求出反比例函数的解析式,求出A的坐标,把A、B的坐标代入一次函数的解析式,即可求出解析式;
(2)求出CO=2,根据三角形面积公式求出即可;
(3)设P点的坐标为P(a,0)根据S△PAC=S△BOC得出![]() PC×4=2,求出PC即可.
PC×4=2,求出PC即可.
试题解析:(1)过B作x轴的垂线,垂足为D,
∵B的坐标为(n,-2),
∴BD=2,
∵tan∠BOC=![]() ,
,
∴OD=4,
∴B的坐标为(-4,-2)
把B(-4,-2)代入y=![]() 得:k=8,
得:k=8,
∴反比例函数为y=![]() ,
,
把A(2,m)代入y=![]() 得:m=4,
得:m=4,
∴A(2,4),
把A(2,4)和B(-4,-2)代入y=ax+b得:![]()
解得:a=1,b=2,
∴一次函数的解析式为:y=x+2;
(2)在y=x+2中,令y=0,得x=-2,
∴CO=2,
∴S△BOC=![]() COBD=
COBD=![]() ×2×2=2;
×2×2=2;
(3)设P点的坐标为P(a,0)
则由S△PAC=S△BOC得:![]() PC×4=2,
PC×4=2,
∴PC=1,
即||a+2|=1,
解得:a=-3或a=-1,
即P的坐标为(-3,0)或(-1,0).


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
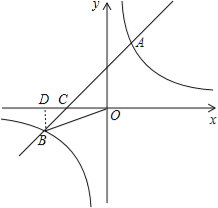
【题目】如图,已知一次函数y=![]() x-3与反比例函数y=
x-3与反比例函数y=![]() 的图象相交于点A(4,n),与x轴相交于点B.
的图象相交于点A(4,n),与x轴相交于点B.

(1)填空:n的值为 ,k的值为 ;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)观察反比函数y=![]() 的图象,当y≥-2时,请直接写出自变量x的取值范围.
的图象,当y≥-2时,请直接写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
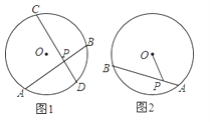
【题目】九年级学生小刚是一个喜欢看书的好学生,他在学习完第二十四章圆后,在家里突然看到爸爸的初中数学书上居然还有一个相交弦定理(圆内的两条相交弦,被交点分成的两条线段长的积相等),非常好奇,仔细阅读原来就是:PAPB=PCPD,小刚很想知道是如何证明的,可异证明部分污损看不清了,只看到辅助线的做法,分别连结AC、BD.聪明的你一定能帮他证出,请在图1中做出辅助线,并写出详细的证明过程.
小刚又看到一道课后习题,如图2,AB是⊙O弦,P是AB上一点,AB=10cm,PA=4cm,OP=5cm,求⊙O的半径,愁坏了小刚,乐于助人的你肯定会帮助他,请写出详细的证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,科技小组准备用材料围建一个面积为60m2的矩形科技园ABCD,其中一边AB靠墙,墙长为12m。设AD的长为xm,DC的长为ym。
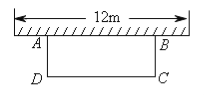
(1)求y与x之间的函数关系式;
(2)若围成矩形科技园ABCD的三边材料总长不超过26m,材料AD和DC的长都是整米数,求出满足条件的所有围建方案。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x>0)交于A(2,4),B(a,1),与x轴,y轴分别交于点C,D.
(x>0)交于A(2,4),B(a,1),与x轴,y轴分别交于点C,D.
(1)直接写出一次函数y=kx+b的表达式和反比例函数y=![]() (x>0)的表达式;
(x>0)的表达式;
(2)求证:AD=BC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E、F、G、H分别是BD、BC、AC、AD的中点,且AB=CD.下列结论:①EG⊥FH,②四边形EFGH是矩形,③HF平分∠EHG,④EG=![]() (BC-AD),⑤四边形EFGH是菱形.其中正确的个数是 ( )
(BC-AD),⑤四边形EFGH是菱形.其中正确的个数是 ( )
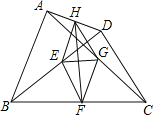
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() 、
、![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 、
、![]() 上,且
上,且![]() ,
,![]() .下列说法中不正确的是( )
.下列说法中不正确的是( )
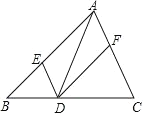
A.四边形![]() 是平行四边形
是平行四边形
B.如果![]() ,那么四边形
,那么四边形![]() 是矩形.
是矩形.
C.如果![]() 平分
平分![]() ,那么四边形
,那么四边形![]() 是正方形.
是正方形.
D.如果![]() 且
且![]() ,那么四边形
,那么四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
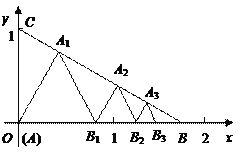
【题目】如图所示,已知:点A(0,0),B(![]() ,0),C(0,1)在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…,则第
,0),C(0,1)在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…,则第![]() 个等边三角形的边长等于__________.
个等边三角形的边长等于__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)根据要求,解答下列问题.
①方程![]() 的解为________________;
的解为________________;
②方程![]() 的解为________________;
的解为________________;
③方程![]() 的解为________________;
的解为________________;
(2)根据以上方程特征及其解的特征,请猜想:
①方程![]() 的解为________________;
的解为________________;
②关于![]() 的方程________________的解为
的方程________________的解为![]() ,
,![]() .
.
(3)请用配方法解方程![]() ,以验证猜想结论的正确性.
,以验证猜想结论的正确性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com