
【题目】如图,已知![]() ,
,![]() .
.
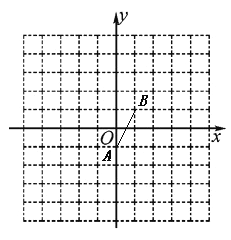
(1)在以下四个格点中,与![]() 、
、![]() 两点不能构成等腰三角形的点是( )
两点不能构成等腰三角形的点是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
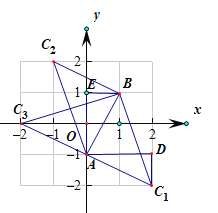
(2)以线段![]() 为直角边作
为直角边作![]() ,
,![]() 为图中所给的格点,这样的
为图中所给的格点,这样的![]() 点有几个?写出它们的坐标.
点有几个?写出它们的坐标.
【答案】(1)C;(2)3个,![]() ,
,![]() ,
,![]()
【解析】
(1)根据等腰三角形的定义及勾股定理判断即可;
(2)根据正方形的性质和全等三角形的判定与性质解答即可.
解:(1)A.此时AB=BP1=![]() ,符合题意;
,符合题意;
B.此时AB=BP1=![]() ,符合题意;
,符合题意;
C.此时三个点构成的是直角三角形,不符合题意;
D.此时AB=AP4=![]() ,符合题意;
,符合题意;
故选C.

(2)当点C![]() 时,
时,
在△ABE和△AC1D中,
∵AE=AD=2,
BE=C1D=1
AB=AC1=![]() ,
,
∴△ABE≌△AC1D,
∴∠C1AD=∠BAE.
∵∠DAE=∠BAE+∠BAD=90°,
∴∠BAC1=∠C1AD+∠BAD=90°,
即△ABC1是以AB为直角边的直角三角形;
同理可求当点C2![]() ,C3
,C3![]() 时,所得三角形也是以AB为直角边的直角三角形.
时,所得三角形也是以AB为直角边的直角三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知Rt△ABC中,AC=BC,∠C=90°,D为AB边中点,∠EDF绕D点旋转,它的两边分别交AC、CB(或它们的延长线)于E、F
(1)当点E在AC边上时(如图1),求证CE=BF
(2)在(1)的条件下,求证:![]()
(3)当∠EDF绕D点旋转到图3的位置即点E、F分别在AC、CB边的延长线上时,上述(2)结论是否成立?若成立,请给予证明;若不成立,![]() 又有怎样的数量关系?请写出你的猜想,不需证明.
又有怎样的数量关系?请写出你的猜想,不需证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子里装着![]() 个黄球,
个黄球,![]() 个黑球和
个黑球和![]() 个红球,他们除了颜色外完全相同.
个红球,他们除了颜色外完全相同.
![]() 小明和小颖玩摸球游戏,规定每人摸球一次再将球放回为依次游戏,若摸到黑球则小明获胜,摸到黄球则小颖获胜,这个游戏公平吗?说说你的理由.
小明和小颖玩摸球游戏,规定每人摸球一次再将球放回为依次游戏,若摸到黑球则小明获胜,摸到黄球则小颖获胜,这个游戏公平吗?说说你的理由.
![]() 现在裁判向袋子中放入若干个红球,大量重复试验后,发现小明获胜的频率稳定在
现在裁判向袋子中放入若干个红球,大量重复试验后,发现小明获胜的频率稳定在![]() 附近,问裁判放入了多少个红球?
附近,问裁判放入了多少个红球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有三个完全相同的小球,分别标有数字3、4、5.从袋子中随机取出一个小球,用小球上的数字作为十位的数字,然后放回;再取出一个小球,用小球上的数字作为个位上的数字,这样组成一个两位数,试问:按这种方法能组成哪些位数?十位上的数字与个位上的数字之和为9的两位数的概率是多少?用列表法或画树状图法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分解因式:
(1)3x2﹣6xy+3y2
(2)﹣3x3y2+6x2y3﹣3xy4
(3)4a2﹣25b2
(4)(2x+3y)(2x﹣y)﹣y(2x﹣y)
(5)x3﹣4x
(6)(m+1)(m﹣9)+8m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,已知三角形的三边长,求这个三角形的面积.
中,已知三角形的三边长,求这个三角形的面积.
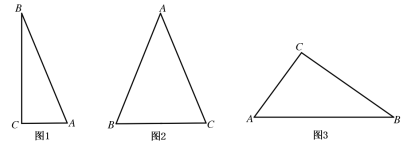
(1)如图1,已知![]() ,
,![]() ,
,![]() ,则
,则![]() 的面积是______;
的面积是______;
(2)如图2,已知![]() ,
,![]() ,求
,求![]() 的面积;
的面积;
(3)如图3,已知![]() ,
,![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB,于点E

(1)求证:△ACD≌△AED;
(2)若∠B=30°,CD=1,求BD的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离和旋转角的度数分别为( )

A.4,30° B.2,60° C.1,30° D.3,60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、
、![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() 轴、
轴、![]() 轴上,且
轴上,且![]() ,
,![]() ,将
,将![]() 绕原点
绕原点![]() 顺时针转动一周,当
顺时针转动一周,当![]() 与直线
与直线![]() 平行时点
平行时点![]() 的坐标为________.
的坐标为________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com