
【题目】如图,在矩形ABCD中,AB=2,AD=![]() ,E是CD边上的中点,P是BC边上的一点,且BP=2CP,连接EP并延长交AB的延长线于点F.
,E是CD边上的中点,P是BC边上的一点,且BP=2CP,连接EP并延长交AB的延长线于点F.
(1)求BF;
(2)判断EB是否平分∠AEC,并说明理由;
(3)连接AP,不添加辅助线,试证明△AEP≌△FBP,直接写出一种经过两次变换的方法使得△AEP与△FBP重合.

【答案】(1)2;(2)EB平分∠AEC,理由见解析(3)①将△BPF绕点P顺时针旋转120°和△EPA重合,再沿PE折叠;②将△BPF以过点P垂直于BC的直线折叠,再绕点P逆时针旋转60°.
【解析】
(1)求出DE,CE,即可得出结论;
(2)用锐角三角函数求出∠AED=60°,得出∠BEC=∠AED=60°,即可得出结论;
(3)先判断出△AEP≌△FBP(AAS),即可得出结论.
解:(1)∵CE∥BF,
∴![]() ,
,
在Rt△ADE中,
∴DE=![]() =
=![]() =1,
=1,
∴CE=1,
∴BF=2;
(2)EB平分∠AEC,理由如下:
在Rt△ADE中,AD=![]() ,DE=1,
,DE=1,
∴tan∠AED=![]() =
=![]() ,
,
∴∠AED=60°,
∴∠BEC=∠AED=60°,
∴∠AEB=180°﹣∠AED﹣∠BEC=60°=∠BEC,
∴EB平分∠AEC;
(3)∵BP=2CP,BC=![]() ,
,
∴CP=![]() ,BP=
,BP=![]() ,
,
在Rt△CEP中,tan∠CEP=![]() ,
,
∴∠CEP=30°,
∴∠BEP=30°,
∴∠AEP=90°,
∵CD∥AB,
∴∠F=∠CEP=30°,
在Rt△ABP中,tan∠BAP=![]() ,
,
∴∠PAB=30°,
∴∠EAP=30°=∠F=∠PAB,
∵CB⊥AF,
∴AP=FP,∠FBP=90°=∠AEP,
在△AEP和△FBP中,  ,
,
∴△AEP≌△FBP(AAS),
变换的方法为:①将△BPF绕点P顺时针旋转120°和△EPA重合,再沿PE折叠;
②将△BPF以过点P垂直于BC的直线折叠,再绕点P逆时针旋转60°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】有![]() 两个黑布袋,
两个黑布袋,![]() 布袋中有四个除标号外完全相同的小球,小球上分别标有数字
布袋中有四个除标号外完全相同的小球,小球上分别标有数字![]() 布袋中有三个除标号外完全相同的小球,小球上分别标有数字
布袋中有三个除标号外完全相同的小球,小球上分别标有数字![]() 小明先从
小明先从![]() 布袋中随机取出一个小球,用
布袋中随机取出一个小球,用![]() 表示取出的球上标有的数字,再从
表示取出的球上标有的数字,再从![]() 布袋中随机取出一个小球,用
布袋中随机取出一个小球,用![]() 来表示取出的球上标有的数字.
来表示取出的球上标有的数字.
(1)若用![]() 表示小明取球时
表示小明取球时![]() 与
与![]() 的对应值,请画出树状图,并写出
的对应值,请画出树状图,并写出![]() 的所有取值;
的所有取值;
(2)求关于![]() 的一元二次方程
的一元二次方程![]() 有实数根的概率.
有实数根的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
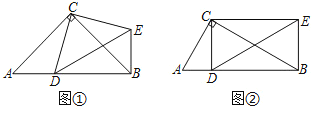
在Rt△ABC中,∠ACB=90°,点D为斜边AB上的动点(不与点A,B重合).
(1)操作发现:如图①,当AC=BC=8时,把线段CD绕点C逆时针旋转90°得到线段CE,连接DE,BE.
①∠CBE的度数为 ;
②当BE= 时,四边形CDBE为正方形;
(2)探究证明:如图②,当BC=2AC时,把线段CD绕点C逆时针旋转90°后并延长为原来的两倍,记为线段CE,连接DE,BE.
①在点D的运动过程中,请判断∠CBE与∠A的大小关系,并证明;
②当CD⊥AB时,求证:四边形CDBE为矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
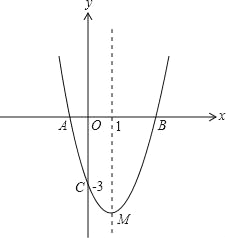
【题目】(11分)如图,抛物线y=ax2+bx﹣3与x轴交于A,B两点,与y轴交于C点,且经过点(2,﹣3a),对称轴是直线x=1,顶点是M.
(1)求抛物线对应的函数表达式;
(2)经过C,M两点作直线与x轴交于点N,在抛物线上是否存在这样的点P,使以点P,A,C,N为顶点的四边形为平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)设直线y=﹣x+3与y轴的交点是D,在线段BD上任取一点E(不与B,D重合),经过A,B,E三点的圆交直线BC于点F,试判断△AEF的形状,并说明理由;
(4)当E是直线y=﹣x+3上任意一点时,(3)中的结论是否成立(请直接写出结论).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A、B两点的坐标分别为(―2,0),(0,1),⊙C的圆心坐标为(0,―1),半径为1.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是( ) 
A. 4 B. ![]() C.
C. ![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
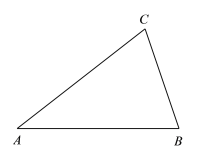
【题目】如图,已知△ABC中,AB=AC.
(1)把△ABC绕点C顺时针旋转得到△DEC,使得点B的对应点E落在AB边上,用尺规作图的方法作出△DEC;(保留作图痕迹,不写作法)
(2)在(1)的条件下,连接AD,求证:AD=BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南宁市金陵镇三联村无公害蔬菜基地有甲、乙两种植户,他们种植了A、B两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
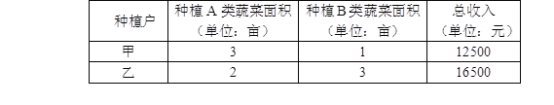
说明:不同种植户种植的同类蔬菜每亩平均收入相等.
(1)求A、B两类蔬菜每亩平均收入各是多少元?
(2)某种植户准备租20亩地用来种植A、B两类蔬菜,为了使总收入不低于63000元,且种植A类蔬菜的面积多于种植B类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所有租种方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)课本情境:如图,已知矩形AOBC,AB=6cm,BC=16cm,动点P从点A出发,以3cm/s的速度向点O运动,直到点O为止;动点Q同时从点C出发,以2cm/s的速度向点B运动,与点P同时结束运动,出发 时,点P和点Q之间的距离是10cm;
(2)逆向发散:当运动时间为2s时,P,Q两点的距离为多少?当运动时间为4s时,P,Q两点的距离为多少?
(3)拓展应用:若点P沿着AO→OC→CB移动,点P,Q分别从A,C同时出发,点Q从点C移动到点B停止时,点P随点Q的停止而停止移动,求经过多长时间△POQ的面积为12cm2?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com