
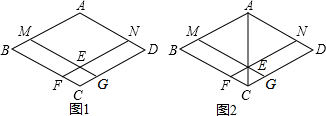
分析 (1)由MG∥AD,NF∥AB,可证得四边形AMEN是平行四边形,又由四边形ABCD是菱形,BM=DN,可得AM=AN,即可证得四边形AMEN是菱形;
(2)易得四边形CGEF是菱形;即可得S△AEM=S△AEN,S△CEF=S△CEG,S△ABC=S△ADC,继而求得答案.
解答 (1)证明:∵MG∥AD,NF∥AB,
∴四边形AMEN是平行四边形,
∵四边形ABCD是菱形,
∴AB=AD,
∵BM=DN,
∴AB-BM=AD-DN,
∴AM=AN,
∴四边形AMEN是菱形;
(2)解:∵四边形AMEN是菱形,
∴S△AEM=S△AEN,
同理:四边形CGEF是菱形,
∴S△CEF=S△CEG,
∵四边形ABCD是菱形,
∴S△ABC=S△ADC,
∴S四边形MBFE=S四边形DNEG,S四边形MBCE=S四边形DNEC,S四边形MBCG=S四边形DNFC,S四边形ABFE=S四边形ADGE,S四边形ABFN=S四边形ADGM.
点评 此题考查了菱形的性质与判定.注意证得四边形AMEN是菱形与四边形CGEF是菱形是关键.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | n2+n | B. | n2+n+1 | C. | n2+2n | D. | n2+2n+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
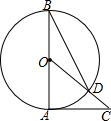 如图,AB是⊙O的直径,AC是⊙O的切线,连接OC与⊙O相交于点D,连接BD,∠C=40°,若点P为优弧$\widehat{ABD}$上的动点,连接PA、PD,则∠APD的大小是25度.
如图,AB是⊙O的直径,AC是⊙O的切线,连接OC与⊙O相交于点D,连接BD,∠C=40°,若点P为优弧$\widehat{ABD}$上的动点,连接PA、PD,则∠APD的大小是25度.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
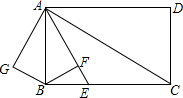 如图在矩形ABCD中,AB=6,AD=8,AE平分∠BAC交BC于点E,过B作BF⊥AE交AE于点F,将△ABF沿AB翻折得到△ABG,将△ABG绕点A逆时针旋转角a,(其中0°<a<180°)记旋转中的△ABG为△AB′G′,在旋转过程中,设直线B′G′分别与直线AD、直线AC交于点M、N,当MA=MN时,线段MD长为8-$\frac{5\sqrt{5}}{2}$.
如图在矩形ABCD中,AB=6,AD=8,AE平分∠BAC交BC于点E,过B作BF⊥AE交AE于点F,将△ABF沿AB翻折得到△ABG,将△ABG绕点A逆时针旋转角a,(其中0°<a<180°)记旋转中的△ABG为△AB′G′,在旋转过程中,设直线B′G′分别与直线AD、直线AC交于点M、N,当MA=MN时,线段MD长为8-$\frac{5\sqrt{5}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com