
【题目】已知,一次函数![]() 的图像与
的图像与![]() 轴、
轴、![]() 轴分别交于点A、点B,与直线
轴分别交于点A、点B,与直线![]() 相交于点C.过点B作
相交于点C.过点B作![]() 轴的平行线l.点P是直线l上的一个动点.
轴的平行线l.点P是直线l上的一个动点.
(1)求点A,点B的坐标.
(2)若![]() ,求点P的坐标.
,求点P的坐标.
(3)若点E是直线![]() 上的一个动点,当△APE是以AP为直角边的等腰直角三角形时,求点E的坐标.
上的一个动点,当△APE是以AP为直角边的等腰直角三角形时,求点E的坐标.

【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 或者
或者![]() ;(3)
;(3)![]() 点坐标为:
点坐标为:![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)由一次函数解析式可直接求解;
(2)由两直线解析式求出交点C的坐标,再由面积相等求出线段BP的长度,继而得出点P的坐标;
(3)设点E(x,![]() ),根据两点间的距离公式求出AP,PE,AE,根据已知条件可得,AP=PE,
),根据两点间的距离公式求出AP,PE,AE,根据已知条件可得,AP=PE,![]() ,列方程组求解即可.
,列方程组求解即可.
解:(1)当x=0时,y=6;当y=0时,x=8,
∴![]() ,
,![]() ;
;
(2)联立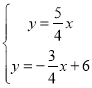
解得: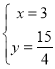 ,
,
∴![]() 为
为![]() .
.
∴![]() .
.
∴![]() ,
,
解得:![]() .
.
∴![]() 或
或![]() .
.
(3)若△APE是以AP为直角边的等腰直角三角形,则有AP=PE,![]() ,设点E坐标为E(x,
,设点E坐标为E(x,![]() ),A(8,0),
),A(8,0),
∵![]() 或
或![]()
∴当![]() 时,有
时,有
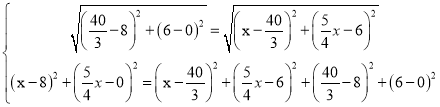
化简求解即可,同理可得出当![]() 时,点E的坐标,
时,点E的坐标,
综上所述,![]() 点坐标为:
点坐标为:![]() 或
或![]() 或
或![]() 或
或![]() .
.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表所示:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法中,错误的是( )
A. 抛物线于x轴的一个交点坐标为(﹣2,0)
B. 抛物线与y轴的交点坐标为(0,6)
C. 抛物线的对称轴是直线x=0
D. 抛物线在对称轴左侧部分是上升的
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的一条弦,OD⊥AB,垂足为点C,交⊙O于点D,点E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度数;
(2)若CD=2,AB=8,求半径的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD为∠BAC的平分线,BM⊥AD,垂足为M,且AB=5,BM=2,AC=9,则∠ABC与∠C的关系为( )

A.∠ABC=2∠CB.∠ABC=![]() ∠CC.
∠CC.![]() ∠ABC=∠CD.∠ABC=3∠C
∠ABC=∠CD.∠ABC=3∠C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】线段AB上有一动点C(不与A,B重合),分别以AC,BC为边向上作等边△ACM和等边△BCN,点D是MN的中点,连结AD,BD,在点C的运动过程中,有下列结论:①△ABD可能为直角三角形;②△ABD可能为等腰三角形;③△CMN可能为等边三角形;④若AB=6,则AD+BD的最小值为![]() . 其中正确的是( )
. 其中正确的是( )

A.②③B.①②③④C.①③④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校有2000名学生,为了解全校学生的上学方式,我校数学兴趣小组在全校随机抽取了150名学生进行抽样调查。整理样本数据,得到下列图表:


(1)若150名学生都在同一个年级抽取,这样的抽样是否合理?_______(填“是”或“否”);
(2)根据调查结果,估计全校2000名学生上学方式的情况:步行______人;骑车_____人;乘公共交通工具_______人; 乘私家车_____人;其它_______人,并绘制成条形统计图;

(3)数学兴趣小组结合调查获取的信息,向学校提出了一些建议。如:骑车上学的学生数约占全校的34%,建议学校合理安排自行车停车场地。请你结合上述统计的全过程,再提出一条合理化建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFMN的一边MN在边BC上,顶点E、F分别在AB、AC上,其中BC=24cm,高AD=12cm.
(1)求证:△AEF∽△ABC:
(2)求正方形EFMN的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设![]() =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;
(3)当∠ABE的正切值是![]() 时,求AB的长.
时,求AB的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com