
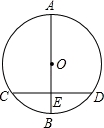
如图,⊙O直径AB垂直于弦CD,垂足E是OB的中点,CD=6cm,则直径AB=__________cm.
科目:初中数学 来源: 题型:
对某校八年级(1)班60名同学的一次数学测验成绩进行统计,如果80.5—90.5分这一组的频数是18,那么这个班的学生这次数学测验成绩在80.5—90.5分之间的频率是( ).
A.18 B.0.3 C.0.4 D.0.35
查看答案和解析>>
科目:初中数学 来源: 题型:
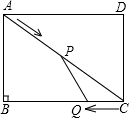
如图,在矩形ABCD中,AB=6米,BC=8米,动点P以2米/秒的速度从点A出发,沿AC向点C移动,同时动点Q以1米/秒的速度从点C出发,沿CB项点B移动,设P、Q两点移动t秒(0<t<5)后,三角形CPQ的面积为S米2.
(1)求面积S与时间t的关系式;
(2)在P、Q两点移动的过程中,四边形ABQP与△CPQ的面积能否相等?若能,求出此时点P的位置;若不能,请说明理由.
(3)t为何值时,三角形CPQ为直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,要测量一条小河的宽度AB的长,可以在小河的岸边作AB的垂线 MN,然后在MN上取两点C,D,使BC=CD,再画出MN的垂线DE,并使点E 与点A,C在一条直线上,这时测得DE的长就是AB的长,其中用到的数学原理是: _ .
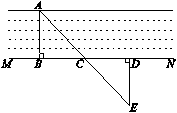
查看答案和解析>>
科目:初中数学 来源: 题型:
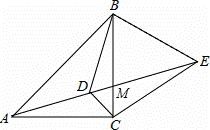
如图,等腰直角△ABC中,CA=CB,点E为△ABC外一点,CE=CA,且CD平分∠ACB交AE于D,且∠CDE=60°.求证:△CBE为等边三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com