
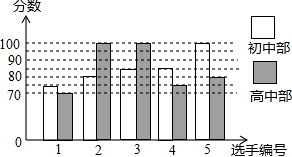
 某中学举行歌手大赛,初、高中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
某中学举行歌手大赛,初、高中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.| 平均数(分) | 中位数(分) | 众数(分) | |
| 初中代表队 | 85 | 85 | 85 |
| 高中代表队 | 85 | 80 | 100 |
分析 (1)根据中位数、平均数、众数的定义即可解决.
(2)根据两个队的平均成绩、中位数的大小即可判断.
(3)比较两个队的方差即可判断.
解答 解:(1)初中队的五次成绩为75,80,85,85,100,故中位数是85.
高中队的平均数=$\frac{70+100+100+75+80}{5}$=85,众数是100.
故答案分别为85,85,100.
(2)从平均数来看两个队的成绩一样,从中位数看初中队成绩好.
(3)高中队的方差为s2=$\frac{1}{5}$[(70-85)2+(100-85)2+(100-85)2+(75-85)2+(80-85)2]=160,
∵初中队的方差为70,70<160,
∴初中队的成绩比较稳定.
点评 本题考查方差、中位数、众数、条形图等众数,记住这些概念是解决问题的关键,理解方差越小成绩越稳定,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在矩形ABCD中,AB=2,BC=4,将BC绕点C逆时针旋转,使点B恰好落在AD边上的点E处,则图中阴影部分(扇形BCE)的面积为$\frac{4π}{3}$.
如图,在矩形ABCD中,AB=2,BC=4,将BC绕点C逆时针旋转,使点B恰好落在AD边上的点E处,则图中阴影部分(扇形BCE)的面积为$\frac{4π}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{10}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
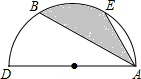 如图,以AD=2为直径的半圆O中,B、E是半圆弧的三等分点,则图中阴影部分的面积为( )
如图,以AD=2为直径的半圆O中,B、E是半圆弧的三等分点,则图中阴影部分的面积为( )| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,滑雪场有一坡角α为20°的滑雪道,滑雪道AC的长为200米,则滑雪道的坡顶到坡底垂直高度AB的长为( )
如图,滑雪场有一坡角α为20°的滑雪道,滑雪道AC的长为200米,则滑雪道的坡顶到坡底垂直高度AB的长为( )| A. | 200tan20°米 | B. | $\frac{200}{sin20°}$米 | C. | 200sin20°米 | D. | 200cos20°米 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
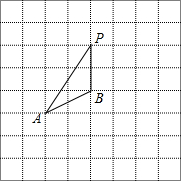 如图,将△ABP放在每个小正方形的边长为1的网格中,点A、B、P均落在格点上.
如图,将△ABP放在每个小正方形的边长为1的网格中,点A、B、P均落在格点上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com