
【题目】阅读下列两则材料,回答问题:
材料一:因为![]() 所以我们将
所以我们将![]() 与
与![]() 称为一対“有理化因式”,有时我们可以通过构造“有理化因式”求值
称为一対“有理化因式”,有时我们可以通过构造“有理化因式”求值
例如:已知![]() ,求
,求![]() 的值
的值
解:![]() ,∵
,∵![]()
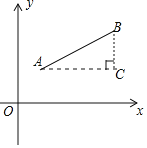
材料二:如图,点A(x1,y1),点B(x2,y2),所以AB为斜边作Rt△ABC,则C(x2,y1),于是AC=|x1﹣x2|,BC=|y1﹣y2|,所以AB=![]() ,反之,可将代数式
,反之,可将代数式![]() 的值看作点(x1,y1)到点(x2,y2)的距离.例如
的值看作点(x1,y1)到点(x2,y2)的距离.例如![]() =
=![]() ,所以可将代数式
,所以可将代数式![]() 的值看作点(x,y)到点(1,﹣1)的距离;
的值看作点(x,y)到点(1,﹣1)的距离;
(1)利用材料一,解关于x的方程:![]() ,其中x≤2;
,其中x≤2;
(2)利用材料二,求代数式![]() 的最小值,并求出此时y与x的函数关系式,写出x的取值范围.
的最小值,并求出此时y与x的函数关系式,写出x的取值范围.
【答案】(1)x=﹣2;(2)y=x+5(﹣3≤x≤1).
【解析】
(1)根据材料一类比计算![]() 的值,利用换元法解方程,可得结论;
的值,利用换元法解方程,可得结论;
(2)把根式下的式子转化成平方+平方的形式,转化成点到点的距离问题,根据两点之间距离最短,所以当三个点共线时距离最短,可以求出最小值和函数关系式.
解:(1)![]() ,
,
![]() ,
,
![]() ;
;
设![]() ,
,
则![]() ,解得:
,解得:![]() ,
,
∴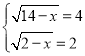 ,
,
∵x≤2,
解得:x=﹣2;
(2)![]() ,
,
![]() ,
,
![]()
![]() ,
,
所以可将![]() 看作点(x,y)到点(1,6)的距离;
看作点(x,y)到点(1,6)的距离;
可将![]() 看作点(x,y)到点(﹣3,2)的距离;
看作点(x,y)到点(﹣3,2)的距离;
∴当代数式![]() 取最小值,
取最小值,
即点(x,y)与点(1,6),(﹣3,2)在同一条直线上,并且点(x,y)位于点(1,6)、(﹣3,2)的中间,
∴![]() 的最小值=
的最小值=![]() ,且﹣3≤x≤1,
,且﹣3≤x≤1,
设过(x,y),(1,6),(﹣3,2)的直线解析式为:y=kx+b,
∴![]() ,
,
解得:![]() ,
,
∴y=x+5(﹣3≤x≤1).


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥CD,∠B=90°,AB=12cm,AD=CD=8cm,动点E从点A出发沿AB以每秒1cm的速度向点B运动,动点F从点B出发沿BA以每秒1cm的速度向点A运动,过点E作AB的垂线交折线AD-DC于点G,以EG、EF为邻边作矩形EFHG,设点E、F运动的时间为t(秒),矩形EFHG与四边形ABCD重叠部分的面积为S(cm2).
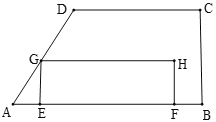
(1)求EG的长(用含t的代数式表示);
(2)当t为何值时,点G与点D重合?
(3)当点G在DC上时,求S(cm2)与t(秒)的函数关系式(S>0);
(4)连接EH、GF、AC、BD,在运动过程中,当这四条线段所在的直线有两条平行时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
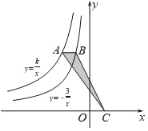
【题目】如图,点A是反比例函数y=![]() 图象上一点,过点A作x轴的平行线交反比例函数y=﹣
图象上一点,过点A作x轴的平行线交反比例函数y=﹣![]() 的图象于点B,点C在x轴上,且S△ABC=
的图象于点B,点C在x轴上,且S△ABC=![]() ,则k=( )
,则k=( )
A. 6B. ﹣6C. ![]() D. ﹣
D. ﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
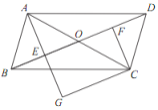
【题目】如图,在□ABCD 中,对角线 AC 与 BD 相交于点 O ,点 E , F 分别为 OB , OD 的中点,延长 AE 至 G ,使 EG =AE ,连接 CG .
(1)求证: △ABE≌△CDF ;
(2)当 AB 与 AC 满足什么数量关系时,四边形 EGCF 是矩形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售一种新型节能产品,现准备从国内和国外两种销售方案中选择一种进行销售.若只在国内销售,销售价格y(元/件)与月销量x(件)的函数关系式为y=![]() x+150,成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为w内(元).若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳
x+150,成本为20元/件,无论销售多少,每月还需支出广告费62500元,设月利润为w内(元).若只在国外销售,销售价格为150元/件,受各种不确定因素影响,成本为a元/件(a为常数,10≤a≤40),当月销量为x(件)时,每月还需缴纳![]() x2元的附加费,设月利润为w外(元).
x2元的附加费,设月利润为w外(元).
(1)当x=1000时,y= 元/件,w内= 元;
(2)分别求出w内,w外与x间的函数关系式(不必写x的取值范围);
(3)当x为何值时,在国内销售的月利润最大?若在国外销售月利润的最大值与在国内销售月利润的最大值相同,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学学生会在开展“厉行勤俭节约,反对铺张浪费”的主题教育活动中,在全校范围内随机抽取了若干名学生就某日晚饭浪费饭菜情况进行调查,调查内容分为四种:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.学生会根据统计结果,绘制了如下统计表:根据所给信息,回答下列问题:
选项 | 频数 | 频率 |
A | 36 | m |
B | n | 0.2 |
C | 6 | 0.1 |
D | 6 | 0.1 |
(1)统计表中:m=______;n=______.
(2)该中学有1800名学生晚饭在校就餐,根据调查结果,估计当天晚饭有多少人能够把饭和菜全部吃完?
(3)为了对同学们浪费的行为进行纠正,校学生会从饭和菜都有剩的甲、乙、丙、丁四名同学中任取2位同学进行批评教育,请用列表法或树状图法求恰好抽到甲和丁的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为发展学生的核心素养,培养学生的综合能力,某学校计划开设四门选修课:乐器、舞蹈、绘画、书法,学校采取随机抽样的方法进行问卷调查![]() 每个被调查的学生必须选择而且只能选择其中一门
每个被调查的学生必须选择而且只能选择其中一门![]() 对调查结果进行整理,绘制成如下两幅不完整的统计图
对调查结果进行整理,绘制成如下两幅不完整的统计图![]() 请结合图中所给信息解答下列问题:
请结合图中所给信息解答下列问题:


![]() 本次调查的学生共有______人,在扇形统计图中,m的值是______.
本次调查的学生共有______人,在扇形统计图中,m的值是______.
![]() 分别求出参加调查的学生中选择绘画和书法的人数,并将条形统计图补充完整.
分别求出参加调查的学生中选择绘画和书法的人数,并将条形统计图补充完整.
![]() 该校共有学生2000人,估计该校约有多少人选修乐器课程?
该校共有学生2000人,估计该校约有多少人选修乐器课程?
查看答案和解析>>
科目:初中数学 来源: 题型:
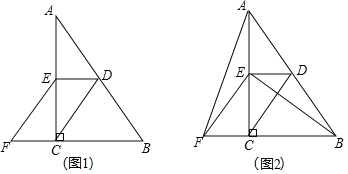
【题目】已知:如图,在![]() 中,
中,![]() ,点D、E分别是AB、AC的中点,点F在BC延长线上,连接EF,且
,点D、E分别是AB、AC的中点,点F在BC延长线上,连接EF,且![]() .
.
![]() 如图1,求证:四边形CDEF是平行四边形;
如图1,求证:四边形CDEF是平行四边形;
![]() 如图2,连接AF、BE,在不添加任何辅助线的情况下,请直接写出图2中所有与
如图2,连接AF、BE,在不添加任何辅助线的情况下,请直接写出图2中所有与![]() 面积相等的三角形.
面积相等的三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学综合实践活动中,小明计划测量城门大楼的高度,在点B处测得楼顶A的仰角为22°,他正对着城楼前进21米到达C处,再登上3米高的楼台D处,并测得此时楼顶A的仰角为45°.
(1)求城门大楼的高度;
(2)每逢重大节日,城门大楼管理处都要在A,B之间拉上绳子,并在绳子上挂一些彩旗,请你求出A,B之间所挂彩旗的长度(结果保留整数).(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com