
【题目】如图,正方形ABCD的边长为2,E在正方形外,![]() ,过D作
,过D作![]() 于H,直线DH,EC交于点M,直线CE交直线AD于点,则下列结论正确的是( )
于H,直线DH,EC交于点M,直线CE交直线AD于点,则下列结论正确的是( )
①![]() ;②
;②![]() ;③
;③![]() ;④若PD=3AD,则MD=
;④若PD=3AD,则MD=![]()
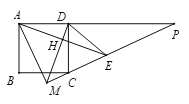
A.1个B.2个C.3个D.4个
【答案】C
【解析】
根据正方形的性质,利用全等的判定和性质、相似的判定和性质、垂直平分线的判定性质、勾股定理等知识对四个结论一一判断即可.
在正方形ABCD中,
AD=DC,
∵DE=DC,
∴AD=DE,
∴∠DAE=∠DEA,
∴①正确;
∵AD=DE,DH⊥AE,
∴DM是AE的垂直平分线,
∴AM=EM,
∴△AMD≌△EMD,
∴∠MAD=∠MED,
∵DE=DC,
∴∠DCE=∠MED,
∴∠MAD=∠DCE,
即∠MAH+∠DAH=∠DME+∠CDM
∵∠DAH+∠ADH=90°,
∠CDM+∠ADH=90°,
∴∠DAH=∠CDM,
∴∠MAH=∠DME,
∵AM=EM,
∴∠MAH=∠MEH,
∴∠DME=∠MEH,
∵DH⊥AE,
∴∠DME=∠MEH=45°,
故②正确;
在EP上截取EN=MC,则△DCM≌△DEN,
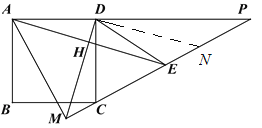
∴∠DNM=∠DME=45°,
∴△DMN是等腰直角三角形,
∴![]() ,
,
∵MN=ME+EN=AM+MC,
∴![]() ,
,
故③正确;
∵PD=3AD,AD=2,
∴PD=6,PA=8,
∵DM是AE的垂直平分线,
且∠DME=45°,
∴∠AMP=90°,
∴△PDC∽△PMA,
∴![]() ,
,
在Rt△PDC中, PC=![]() =2
=2![]() ,
,
在Rt△PAM中,AM=![]() ,PM=
,PM=![]() ,
,
∴CM=![]() ,
,
∵![]() ,
,
∴DM=![]() =
=![]() .
.
故④错误.
故选C.


科目:初中数学 来源: 题型:
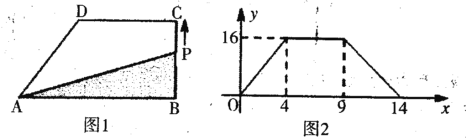
【题目】如图1,在直角梯形ABCD中,动点P从B点出发,沿B→C→D→A匀速运动,设点P运动的路程为x,△ABP的面积为y,图象如图2所示.
(1)当点P运动的路程x=4时,△ABP的面积为y= ;
(2)求:线段AB的长;
(3)求:梯形ABCD的面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列两个三角形中,一定全等的是()
A. 两个等边三角形
B. 有一个角是![]() ,腰相等的两个等腰三角形
,腰相等的两个等腰三角形
C. 有一条边相等,有一个内角相等的两个等腰三角形
D. 有一个角是![]() ,底相等的两个等腰三角形
,底相等的两个等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将坐标原点O沿x轴向左平移2个单位长度得到点A,过点A作y轴的平行线交反比例函数y=![]() 的图象于点B,AB=
的图象于点B,AB=![]() .
.
(1)求反比例函数的解析式;
(2)若P(x1,y1)、Q(x2,y2)是该反比例函数图象上的两点,且x1<x2时,y1>y2,指出点P、Q各位于哪个象限?并简要说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.
(1)求证:△ABC≌△AED;
(2)当∠B=140°时,求∠BAE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了![]() 名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如下统计图表:
名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如下统计图表:


根据以上提供的信息,解答下列问题:
(1)![]() ______,
______,![]() ______,
______,![]() ______;
______;
(2)补全上面的条形统计图;
(3)若该校共有学生1000名.根据抽样调查结果,估计该校最喜爱《中国诗词大会》节目的学生有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知;如图1,菱形ABCD的边AB在x轴上,点B的坐标为![]() ,点C在y轴上,
,点C在y轴上,![]() .
.
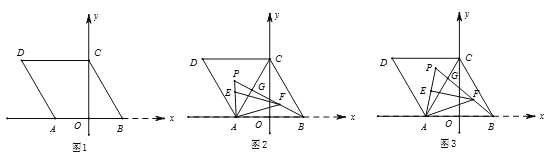
(1)求点A的坐标;
(2)如图2,连接AC,点P为△ACD内一点,BP与AC交于点G,![]() ,点E、F分别在线段AP、BP上,且
,点E、F分别在线段AP、BP上,且![]() .若
.若![]() ,求
,求![]() 的值;
的值;
(3)如图3,在(2)的条件下,当![]() 时,试判断△PAF形状并说明理由.
时,试判断△PAF形状并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC的垂直平分线EF交∠ABC的平分线BD于E,如果∠BAC=60°,∠ACE=24°,那么∠ABC的大小是( )
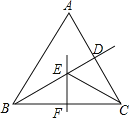
A.32°B.56°C.64°D.70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:(一)如果我们能找到两个实数x、y使![]() 且
且![]() ,这样
,这样![]() ,那么我们就称
,那么我们就称![]() 为“和谐二次根式”,则上述过程就称之为化简“和谐二次根式”.
为“和谐二次根式”,则上述过程就称之为化简“和谐二次根式”.
例如:![]() .
.
(二)在进行二次根式的化简与运算时,我们有时还会碰上如![]() 一样的式子,其实我们还可以将其进一步化简:
一样的式子,其实我们还可以将其进一步化简: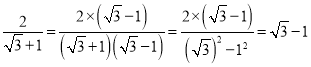 ,那么我们称这个过程为分式的分母有理化.
,那么我们称这个过程为分式的分母有理化.
根据阅读材料解决下列问题:
(1)化简“和谐二次根式”:①![]() ___________,②___________;
___________,②___________;
(2)已知![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)设![]() 的小数部分为
的小数部分为![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com