
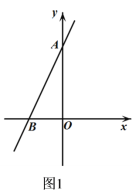
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�ֱ��AB�ֱ�y�ᡢx���ڵ�A��0��a������B��b��0������a��b����a2-4a+4+![]() ��0��
��0��
��1����a��b��ֵ��
��2����ABΪ����Rt��ABC����C��ֱ��AB���Ҳ࣬�ҡ�ACB��45�������C�����ꣻ
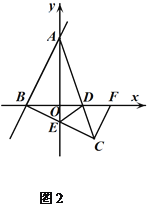
��3������2���ĵ�C�ڵ������ޣ���ͼ2����AC�� x�ύ�ڵ�D��BC��y�ύ�ڵ�E������ DE������C��CF��BC��x���ڵ�F��
����֤��CF=![]() BC��
BC��
��ֱ��д����C��DE�ľ��룮
���𰸡���1��a��2��b��-1����2�����������ĵ�C��2��1����1��-1������3����֤������������1��
��������
��1���ɵ�(a2)2+![]() ��0���ɷǸ��������ʿɵó��𰸣�
��0���ɷǸ��������ʿɵó��𰸣�
��2���������������BAC=90�����ABC=90�������ݵ���ֱ�������ε����ʼ�ȫ�������ε����ʿ������C�����ꣻ
��3������ͼ3������C��CL��y���ڵ�L����CL=1=BO������AAS��֤����BOE�ա�CLE���ó�BE=CE������ASA��֤����ABE�ա�BCF���ó�BE=CF������۵�֤��
����ͼ4������C��CK��ED�ڵ�K������C��CH��DF�ڵ�H������SAS��֤����CDE�ա�CDF���ɵá�BAE=��CBF���ɽ�ƽ���ߵ����ʿɵ�CK=CH=1��
��1����a24a+4+![]() ��0��
��0��
��(a2)2+![]() ��0��
��0��
�ߣ�a-2��2��0��![]() ��0��
��0��
��a-2=0��2b+2=0��
��a=2��b=-1��
��2���ɣ�1��֪a=2��b=-1��
��A��0��2����B��-1��0����
��OA=2��OB=1��
�ߡ�ABC��ֱ�������Σ��ҡ�ACB=45����
��ֻ�С�BAC=90�����ABC=90����
��������BAC=90��ʱ����ͼ1��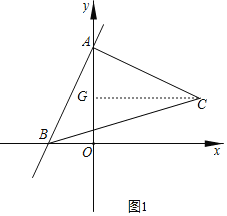
�ߡ�ACB=��ABC=45����
��AB=CB��
����C��CG��OA��G��
���CAG+��ACG=90����
�ߡ�BAO+��CAG=90����
���BAO=��ACG��
����AOB����BCP�� ��
��
���AOB�ա�CGA��AAS����
��CG=OA=2��AG=OB=1��
��OG=OA-AG=1��
��C��2��1����
��������ABC=90��ʱ����ͼ2��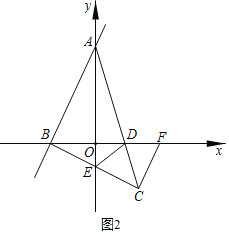
ͬ���ķ����ã�C��1��-1����
�������������ĵ�C��2��1����1��-1��
��3������ͼ3���ɣ�2��֪��C��1��-1����
����C��CL��y���ڵ�L����CL=1=BO��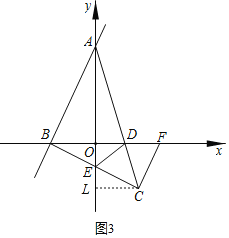
����BOE����CLE��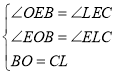 ��
��
���BOE�ա�CLE��AAS����
��BE=CE��
�ߡ�ABC=90����
���BAO+��BEA=90����
�ߡ�BOE=90����
���CBF+��BEA=90����
���BAE=��CBF��
����ABE����BCF�� ��
��
���ABE�ա�BCF��ASA����
��BE=CF��
��CF��![]() BC��
BC��
�ڵ�C��DE�ľ���Ϊ1��
��ͼ4������C��CK��ED�ڵ�K������C��CH��DF�ڵ�H��
�ɢ�֪BE=CF��
��BE=![]() BC��
BC��
��CE=CF��
�ߡ�ACB=45������BCF=90����
���ECD=��DCF��
��DC=DC��
���CDE�ա�CDF��SAS����
���BAE=��CBF��
��CK=CH=1��


 ��Կ���Ծ�ϵ�д�
��Կ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ڡ�ACB�͡�AED�У�AC=BC��AE=DE����ACB=��AED=90�㣬��E��AB�ϣ�F���߶�BD���е㣬����CE��FE��
��1����AD=3![]() ��BE=4����EF�ij���
��BE=4����EF�ij���
��2����֤��CE=![]() EF��
EF��
��3����ͼ1�еġ�AED�Ƶ�A˳ʱ����ת��ʹAED��һ��AEǡ�����ACB�ı�AC��ͬһ��ֱ���ϣ���ͼ2��������BD��ȡBD���е�F���ʣ�2���еĽ����Ƿ���Ȼ��������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB����O��ֱ����PO��AB��PE����O�����ߣ���AB���ӳ����ڵ�C���е�ΪE��AE��PO�ڵ�F��
��1����֤��![]() PEF�ǵ��������Σ�
PEF�ǵ��������Σ�
��2����ͼ�У���EH��AB������ΪH������BD��PC����EH�ڵ�G����EG=5��sinC=![]() ����ֱ��AB�ij���
����ֱ��AB�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=1����A=60����EFGH�Ǿ��Σ����εĶ��㶼�����εı��ϣ���AE=AH=x��0��x��1�������ε����ΪS��
��1����S����x�ĺ�������ʽ��
��2����EFGH��������ʱ����S��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ſ���������˶���������ĩ��Լ�����������̵������ܲ�����.
��1����������![]() �㣬�ſ����ͬʱ�Ӽҳ������ֱ������г��Ͳ��е���Ҿ���ֱ�Ϊ
�㣬�ſ����ͬʱ�Ӽҳ������ֱ������г��Ͳ��е���Ҿ���ֱ�Ϊ![]() ǧ��
ǧ��![]() ǧ���̵�����·��ڻ�ϣ����ͬʱ������ſ�ÿ���ӱ��ÿ���Ӷ���
ǧ���̵�����·��ڻ�ϣ����ͬʱ������ſ�ÿ���ӱ��ÿ���Ӷ���![]() �ף����ſ�������ٶȷֱ��Ƕ�����
�ף����ſ�������ٶȷֱ��Ƕ�����![]() �֣�
�֣�
��2�����˵����̵���Լ������![]() ǧ������Ϣ������ܲ��ٶ����ſ��ܲ��ٶȵ�
ǧ������Ϣ������ܲ��ٶ����ſ��ܲ��ٶȵ�![]() ����������ͬ��㣬ͬʱ�����������ȵ�Ŀ�ĵ�
����������ͬ��㣬ͬʱ�����������ȵ�Ŀ�ĵ�![]() ����.
����.
�ٵ�![]() ��
��![]() ʱ��������˶��ٷ��ӣ�
ʱ��������˶��ٷ��ӣ�
�����ſ����ܲ��ٶȶ�����![]() �֣���ֱ���ú�
�֣���ֱ���ú�![]() ��
��![]() ��ʽ�ӱ�ʾ��
��ʽ�ӱ�ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=-x+2�ֱ�x�ᡢy���ڵ�A��B����D��BA���ӳ����ϣ�OD�Ĵ�ֱƽ���߽��߶�AB�ڵ�C������OBC����OAD���ܳ���ȣ���OD�ij���( )
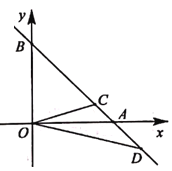
A. 2B. 2![]() C.
C. ![]() D. 4
D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ǰС����1200Ԫ��ũó�г����������۷ֱ�Ϊÿ��30Ԫ��50Ԫ��A,B����ˮ���������ۣ����ֱ���ÿ��35Ԫ��60Ԫ�ļ۸���ۣ��蹺��Aˮ��x�䣬Bˮ��y��.
(1)��С����ˮ��ȫ���۳�����215Ԫ����С��������A��Bˮ����������?
(2)��Ҫ��Aˮ����������������Bˮ������������Ӧ����η��乺��A, Bˮ����������ȫ���۳����ܻ���������ʱ��������Ƕ���?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���֪����������y��![]() x��ͼ���뷴��������y��
x��ͼ���뷴��������y��![]() ��ͼ����A��a����2����B���㣮
��ͼ����A��a����2����B���㣮
��1�����������ı���ʽ�͵�B�����ꣻ
��2��P�ǵ�һ�����ڷ���������ͼ����һ�㣬����P��y���ƽ���ߣ���ֱ��AB�ڵ�C������PO������POC�����Ϊ3�����P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����A��x1��y1����B��x2��y2������ij����ͼ���ϣ��ҵ�x1��x2��0ʱ��y1��y2����˺���һ�����ǣ�������
A. ![]() B. y����2x+1 C. y��x2��1 D.
B. y����2x+1 C. y��x2��1 D. ![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com