【题目】如图，根据要求回答下列问题：
（1）点A关于y轴对称点A′的坐标是 ；点B关于y轴对称点B′的坐标是
（2）作出△ABC关于y轴对称的图形△A′B′C′（不要求写作法）
（3）求△ABC的面积．
【答案】（1）（3，2），（4，﹣3）；（2）图形见解析（3）
【解析】试题分析：
（1）对照图形可知点A、B的坐标分别：（-3，2）、（-4，-3），由此写出点A′、B′的坐标即可；
（2）分别作出点A、B、C关于y轴的对称点A′、B′、C′，再顺次连接这三点即可得到所求三角形；
（3）如图，由S△ABC=S矩形DBEF-S△ADB-S△BEC-S△AFC，计算出△ABC的面积即可.
试题解析：
（1）由图可知：点A、B的坐标分别：（-3，2）、（-4，-3），
∴点A、B关于y轴的对称点A′和B′的坐标分别为：（3，2），（4，﹣3）；
（2）如下图所示；△A′B′C′为所求的图形；
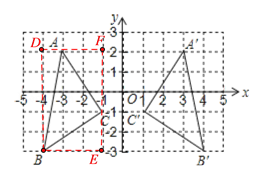
（3）如图：
S△ABC=S矩形DBEF-S△ADB-S△BEC-S△AFC
=
=
=
．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
【题目】如图,已知A(3，0),B(0，-1)，连接AB,过B点作AB的垂线段,使BA=BC,连接AC.
(1)如图1，求C点坐标；
(2)如图2,若P点从A点出发,沿x轴向左平移,连接BP,作等腰直角三角形△BPQ,连接CQ.求证:PA=CQ.
(3)在(2)的条件下,若C、P、Q三点共线,求此时P点坐标及∠APB的度数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△AOB中，∠AOB=90°，OA=3，OB=2，将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE，将线段EF绕点E逆时针旋转90°后得线段ED，分别以O，E为圆心，OA、ED长为半径画弧AF和弧DF，连接AD，则图中阴影部分面积是（ ）
A. π B. 
C. 3+π D. 8﹣π
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下列材料：
（1）解方程： 
解：方程化为： 
.
即化为：（2x-3）（x-1）=0，
∴ 2x-3=0或x-1=0，
解得：x=
或x=1.
∴方程的根为： 
， 
.
（2）求解分式方程的过程是：将分式方程化为整式方程，然后求解整式方程，然后将整工方程的根代入验根，舍去增根，得到的根就是原方程的根.
参考上述材料，解决下列问题：
（1）解方程： 
；
（2）若方程
的一个解是x=1，则方程的其他解是__________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，海上有一灯塔P，在它周围3海里处有暗礁.一艘客轮以9海里/时的速度由西向东航行，行至A点处测得P在它的北偏东60度的方向，继续行驶20分钟后，到达B处又测得灯塔P在它的北偏东45度方向. 问客轮不改变方向继续前进有无触礁的危险?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在□ABCD中，E、F分别是AB、CD的中点，AF与DE相交于点G，CE与BF相交于点H．
（1）求证：四边形EHFG是平行四边形；
（2）若四边形EHFG是矩形，则□ABCD应满足的条件是 （不需要证明）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com