【题目】当你去看电影的时候，你想坐得离屏幕近一些，可是又不想为了看屏幕边缘的镜头不停地转动眼睛．如图所示，点A、B分别为屏幕边缘两点，若你在P点，则视角为∠APB.如果你觉得电影院内P点是观看的最佳位置，可是已经有人坐在那了，那么你会找到一个位置Q，使得在Q、P两点有相同的视角吗？请在图中画出来(保留画图痕迹，不写画法)．
备战中考寒假系列答案科目：初中数学 来源： 题型：
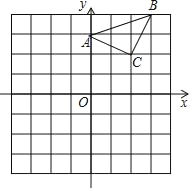
【题目】已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A（0，3）、B（3，4）、C（2，2）（正方形网格中每个小正方形的边长是一个单位长度）．
（1）画出△ABC向下平移4个单位长度得到的△A1B1C1，点C1的坐标是 ；
（2）以点B为位似中心，在网格内画出△A2B2C2，使△A2B2C2与△ABC位似，且位似比为2：1，点C2的坐标是 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知函数y=ax2+bx+c（a≠0）的图象如图，下列5个结论，其中正确的结论有（ ）
①abc＜0
②3a+c＞0
③4a+2b+c＜0
④2a+b=0
⑤b2＞4ac
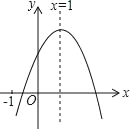
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察下表：
则一元二次方程x2-2x-2=0在精确到0.1时一个近似根是______，利用抛物线的对称性，可推知该方程的另一个近似根是_______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】抛物线
上部分点的横坐标
，纵坐标
的对应值如下表：
| … |
|
|
|
|
| … |
| … |
|
|
|
|
| … |
小聪观察上表，得出下面结论：①抛物线与
轴的一个交点为
；②函数的最大值为
；③抛物线的对称轴是
；④在对称轴左侧，随增大而增大．其中正确有（ ）
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，某大学的楼门是一抛物线形水泥建筑物，大门的地面宽度为
，两侧距离地面
高处各有一个挂校名横匾用的铁环，两铁环的水平距离为
，则校门的高约为(精确到
，水泥建筑物的厚度忽略不计)( )
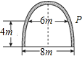
A. 9.2m B. 9.1m C. 9.0m D. 8.9m
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知MN∥EF∥BC，点A、D为直线MN上的两动点，AD＝a，BC＝b，AE∶ED＝m∶n；
(1)当点A、D重合，即a＝0时(如图1)，试求EF.(用含m，n，b的代数式表示)
(2)请直接应用(1)的结论解决下面问题：当A、D不重合，即a≠0，
①如图2这种情况时，试求EF.(用含a，b，m，n的代数式表示)
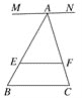
图1
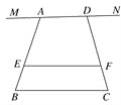
图2
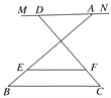
图3
②如图3这种情况时，试猜想EF与a、b之间有何种数量关系？并证明你的猜想．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数y=ax2+bx+c的图象如图所示，则下列结论：①ac＞0；②a﹣b+c＜0；③当x＜0时，y＜0；④方程ax2+bx+c=0（a≠0）有两个大于﹣1的实数根．其中正确的结论有（ ）
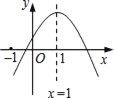
A. ①③ B. ②③ C. ①④ D. ②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
