
分析 结合分式混合运算的运算法则进行求解即可.
解答 解:(1)原式=4x2+y2-4xy+4xy-2x2-x2+y2
=4x2+y2-2x2-x2+y2
=x2+2y2.
(2)原式=$\frac{(x-2y)^{2}}{x(x-y)}$÷($\frac{{x}^{2}-{y}^{2}-3{y}^{2}}{x-y}$)+$\frac{1}{x}$
=$\frac{(x-2y)^{2}}{x(x-y)}$÷$\frac{{x}^{2}-4{y}^{2}}{x-y}$+$\frac{1}{x}$
=$\frac{(x-2y)^{2}}{x({x}^{2}-4{y}^{2})}$+$\frac{1}{x}$
=$\frac{x-2y}{x(x+2y)}$+$\frac{1}{x}$
=$\frac{x-2y+(x+2y)}{x(x+2y)}$
=$\frac{2}{x+2y}$.
点评 本题考查了分式的混合运算,解答本题的关键在于熟练掌握有分式混合运算的运算法则.


科目:初中数学 来源: 题型:解答题
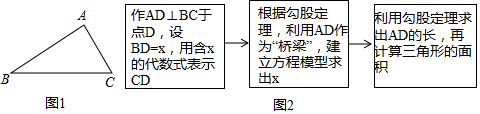
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,路灯(P点)距地面9米,身高1.5米的小云从距路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?
如图,路灯(P点)距地面9米,身高1.5米的小云从距路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
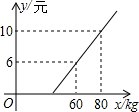 某地长途汽车客运公司规定每位旅客可随身携带一定的行李,如果超出规定,那么需要购买行李票,行李票 y(元)是行李质量 x(kg)的一次函数,其图象如图.
某地长途汽车客运公司规定每位旅客可随身携带一定的行李,如果超出规定,那么需要购买行李票,行李票 y(元)是行李质量 x(kg)的一次函数,其图象如图.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=2,则△A6B6A7的边长为64.
如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=2,则△A6B6A7的边长为64.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
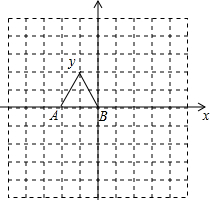 如图,在边长均为1的小正方形网格纸中,△OAB的顶点0、A、B均在格点上,且O是直角坐标系的原点,点A在x轴上.
如图,在边长均为1的小正方形网格纸中,△OAB的顶点0、A、B均在格点上,且O是直角坐标系的原点,点A在x轴上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com