
【题目】△ABC 中,AB=AC,过其中一个顶点的直线可以把这个三角形分成另外两个等腰三角形,则∠BAC( )
A. 36°,90°,![]() , 108°B. 36°,72°,
, 108°B. 36°,72°,![]() ,90°
,90°
C. 90°,72°,108°,![]() D. 36°,90°,108°,
D. 36°,90°,108°,![]()
【答案】A
【解析】
利用三角形内角和定理求解.由于本题中经过等腰三角形顶点的直线没有明确是经过顶角的顶点还是底角的顶点,因此本题要分情况讨论.
①如图1,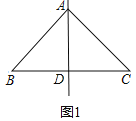
当过顶角的顶点的直线把它分成了两个等腰三角形,则AB=AC,AD=CD=BD,
设∠B=x°,
则∠BAD=∠B=x°,∠C=∠B=x°,
∴∠CAD=∠C=x°,
∵∠B+∠BAC+∠C=180°,
∴x+x+x+x=180,
解得x=45,
则顶角是90°;
②如图2,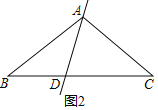
AB=AC=CD,BD=AD,
设∠C=x°,
∵AB=AC,
∴∠B=∠C=x°,
∵BD=AD,
∴∠BAD=∠B=x°,
∴∠ADC=∠B+∠BAD=2x°,
∵AC=CD,
∴∠CAD=∠ADC=2x°,
∴∠BAC=3x°,
∴x+x+3x=180,x=36°,则顶角是108°.
③如图3,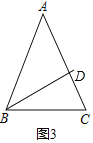
当过底角的角平分线把它分成了两个等腰三角形,则有AB=AC,BC=BD=AD,
设∠BAC=x°,
∵BD=AD,
∴∠ABD=∠BAC=x°,
∴∠CDB=∠ABD+∠BAC=2x°,
∵BC=BD,
∴∠C=∠CDB=2x°,
∵AB=AC,
∴∠ABC=∠C=2x°,
∵∠BAC+∠ABC+∠C=180°,
∴x+2x+2x=180,
x=36,
则顶角是36°.
④如图4,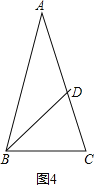
当∠BAC=x°,∠ABC=∠ACB=3x°时,也符合,
AD=BD,BC=DC,
∠BAC=∠ABD=x,∠DBC=∠BDC=2x,
则x+3x+3x=180°,
x=(![]() )°
)°
则∠BAC=90°或108°或36°或(![]() )°.
)°.
故选:A.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
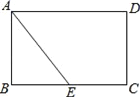
【题目】如图,现有一张矩形纸片ABCD,其中AB=4cm,BC=6cm,点E是BC的中点.将纸片沿直线AE折叠,使点B落在梯形AECD内,记为点B′,那么B′、C两点之间的距离是______ cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
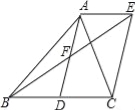
【题目】如图,AD是△ABC的中线,AE∥BC,BE交AD于点F,且AF=DF.
(1)求证:四边形ADCE是平行四边形;
(2)当AB、AC之间满足 时,四边形ADCE是矩形;
(3)当AB、AC之间满足 时,四边形ADCE是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
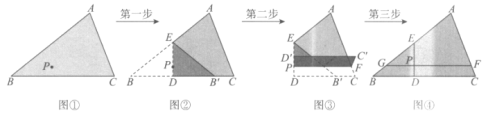
【题目】已知:如图①所示的三角形纸片内部有一点P.
任务:借助折纸在纸片上画出过点P与BC边平行的线段FG.
阅读操作步骤并填空:
小谢按图①~图④所示步骤进行折纸操作完成了画图任务.
在小谢的折叠操作过程中,
(1)第一步得到图②,方法是:过点P折叠纸片,使得点B落在BC边上,落点记为![]() ,折痕分别交原AB,BC边于点E,D,此时∠
,折痕分别交原AB,BC边于点E,D,此时∠![]() 即∠
即∠![]() =__________°;
=__________°;
(2)第二步得到图③,参考第一步中横线上的叙述,第二步的操作指令可叙述为:_____________,并求∠EPF的度数;
(3)第三步展平纸片并画出两次折痕所在的线段ED,FG得到图④.
完成操作中的说理:
请结合以上信息证明FG∥BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 P 是∠AOB 内部一定点
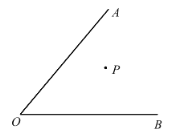
(1)若∠AOB=50°,作点 P 关于 OA 的对称点 P1,作点 P 关于 OB 的对称点 P2,连 OP1、OP2,则∠P1OP2=___.
(2)若∠AOB=α,点 C、D 分别在射线 OA、OB 上移动,当△PCD 的周长最小时,则∠CPD=___(用 α 的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线 y=a(x﹣2)![]() +1 经过点 P(1,﹣3)
+1 经过点 P(1,﹣3)
(1)求 a 的值;
(2)若点 A(m,y![]() )、B(n ,y
)、B(n ,y![]() )(m<n<2)都在该抛物线上,试比较 y
)(m<n<2)都在该抛物线上,试比较 y![]() 与y
与y![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生对“安全常识”的掌握程度,随机抽取部分学生安全知识竞赛的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.图中A表示“不了解”,B表示“了解很少”、C表示“基本了解”,D表示“非常了解”.请根据统计图所提供的信息解答下列问题:
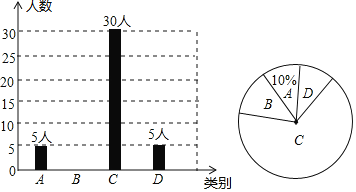
(1)被调查的总人数是 人,扇形统计图中A部分所对应的扇形圆心角的度数为 度;
(2)补全条形统计图;
(3)若该校共有学生1500人,请根据上述调查结果,估计该校学生中达到“基本了解”和“非常了解”共有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
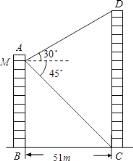
【题目】如图所示,两个建筑物AB和CD的水平距离为51m,某同学住在建筑物AB内10楼M室,他观测建筑物CD楼的顶部D处的仰角为30°,测得底部C处的俯角为45°,求建筑物CD的高度.(![]() 取1.73,结果保留整数)
取1.73,结果保留整数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com