
分析 根据两直线相交的问题,把(2,3)分别代入y=a1x+b1和y=a2x+b2得2a1+b1=3,2a2+b2=3,两式相减得到b1-b2=-2(a1-a2),设过点(a1,b1)和(a2,b2)的一次函数的表达式为y=mx+n,则$\left\{\begin{array}{l}{m{a}_{1}+n={b}_{1}}\\{m{a}_{2}+n={b}_{2}}\end{array}\right.$,把两方程相减得到m(a1-a2)=b1-b2,则可求出m=-2,所以n=2a1+b1=3,于是得到过点(a1,b1)和(a2,b2)的一次函数的表达式为y=-2x+3.
解答 解:把(2,3)分别代入y=a1x+b1和y=a2x+b2得2a1+b1=3,2a2+b2=3,则b1-b2=-2(a1-a2),
设过点(a1,b1)和(a2,b2)的一次函数的表达式为y=mx+n,
则$\left\{\begin{array}{l}{m{a}_{1}+n={b}_{1}}\\{m{a}_{2}+n={b}_{2}}\end{array}\right.$,
m(a1-a2)=b1-b2
所以m=-2,
-2a1+n=b1,即n=2a1+b1=3,
所以过点(a1,b1)和(a2,b2)的一次函数的表达式为y=-2x+3.
故答案为y=-2x+3.
点评 本题考查了两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | x2+x-1=0 | B. | x2+1=0 | C. | x2-x+2=0 | D. | $\frac{x}{x-1}=\frac{1}{x-1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
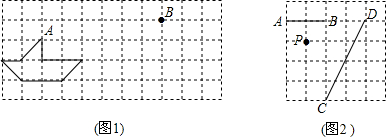
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB是⊙O的直径,CD是弦,AB⊥CD,垂足为点E,连接OD、CB、AC,∠ODE=30°,EB=2,那么CD的长为( )
如图,AB是⊙O的直径,CD是弦,AB⊥CD,垂足为点E,连接OD、CB、AC,∠ODE=30°,EB=2,那么CD的长为( )| A. | 4$\sqrt{3}$ | B. | 5$\sqrt{3}$ | C. | 5$\sqrt{5}$ | D. | 6$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
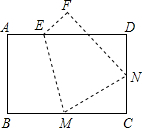 如图,将矩形ABCD沿EM折叠,使顶点B恰好落在CD边的中点N上.若AB=6,AD=9,则五边形ABMND的周长为( )
如图,将矩形ABCD沿EM折叠,使顶点B恰好落在CD边的中点N上.若AB=6,AD=9,则五边形ABMND的周长为( )| A. | 28 | B. | 26 | C. | 25 | D. | 22 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
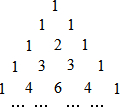 如图所示的“贾宪三角”告诉了我们二项式乘方展开式的系数规律,如:第四行的四个数恰好对应着(a+b)3的展开式a3+3a2b+3ab2+b3的系数; 第五行的五个数恰好对应着(a+b)4的展开式a4+4a3b+6a2b2+4ab3+b4的系数;
如图所示的“贾宪三角”告诉了我们二项式乘方展开式的系数规律,如:第四行的四个数恰好对应着(a+b)3的展开式a3+3a2b+3ab2+b3的系数; 第五行的五个数恰好对应着(a+b)4的展开式a4+4a3b+6a2b2+4ab3+b4的系数;查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 四个规模不同的滑梯A,B,C,D,它们的滑板长(平直的)分别为300m,250m,200m,200m;滑板与地面所成的角度分别为30°,45°,45°,60°,则关于四个滑梯的高度正确说法( )
四个规模不同的滑梯A,B,C,D,它们的滑板长(平直的)分别为300m,250m,200m,200m;滑板与地面所成的角度分别为30°,45°,45°,60°,则关于四个滑梯的高度正确说法( )| A. | A的最高 | B. | B的最高 | C. | C的最高 | D. | D的最高 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com