
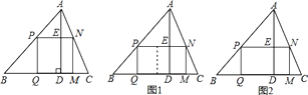
【题目】课本中有一道作业题:有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)加工成的正方形零件的边长是多少mm?
(2)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少?请你计算.
(3)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.
【答案】![]() 加工成的正方形零件的边长是
加工成的正方形零件的边长是![]() ;
;![]() 这个矩形零件的两条边长分别为
这个矩形零件的两条边长分别为![]() ,
,![]() ;
;![]() 的最大值为
的最大值为![]() ,此时
,此时![]() ,
,![]() .
.
【解析】
(1)设正方形的边长为xmm,则PN=PQ=ED=x,AE=ADED=80x,通过证明△APN∽△ABC,利用相似比可得到![]() ,然后根据比例性质求出x即可;
,然后根据比例性质求出x即可;
(2)由于矩形是由两个并排放置的正方形所组成,则可设PQ=x,则PN=2x,AE=80x,然后与(1)的方法一样求解;
(3)设PN=x,用PQ表示出AE的长度,然后根据相似三角形对应高的比等于相似比列出比例式并用x表示出PN,然后根据矩形的面积公式列式计算,再根据二次函数的最值问题解答.
(1)如图![]() ,
,
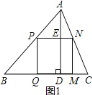
设正方形的边长为![]() ,则
,则![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
解得![]() .
.
∴加工成的正方形零件的边长是![]() ;
;
![]() 如图
如图![]() ,
,
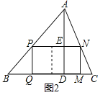
设![]() ,则
,则![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
解得:![]() ,
,
∴![]() ,
,
∴这个矩形零件的两条边长分别为![]() ,
,![]() ;
;
![]() 如图
如图![]() ,
,
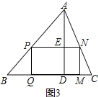
设![]() ,矩形
,矩形![]() 的面积为
的面积为![]() ,
,
由条件可得![]() ,
,
∴![]() ,
,
即![]() ,
,
解得:![]() .
.
则![]() ,
,
故![]() 的最大值为
的最大值为![]() ,此时
,此时![]() ,
,![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,一个长方体形盒子的长、宽、高分别为4cm,4cm,6cm
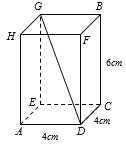
(1)一只蚂蚁想从盒底的点A沿盒的表面爬到盒顶的点B,请你帮蚂蚁设计一条最短的路线,蚂蚁要爬行的最短路线是多少?
(2)若将一根木棒放进盒子里并能盖上盖子,则能放入该盒子里的木棒的最大长度是多少cm ? (结果可保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在第1个△ABA1中,∠B=40°,∠BAA1=∠BA1A,在A1B上取一点C,延长AA1到A2,使得在第2个△A1CA2中,∠A1CA2=∠A1 A2C;在A2C上取一点D,延长A1A2到A3,使得在第3个△A2DA3中,∠A2DA3=∠A2 A3D;…,按此做法进行下去,第3个三角形中以A3为顶点的内角的度数为 ;第n个三角形中以An为顶点的内角的度数为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王大伯要做一张如图所示的梯子,梯子共有![]() 级互相平行的踏板,每相邻两级踏板之间的距离都相等.已知梯子最上面一级踏板的长度
级互相平行的踏板,每相邻两级踏板之间的距离都相等.已知梯子最上面一级踏板的长度![]() ,最下面一级踏板的长度
,最下面一级踏板的长度![]() .则
.则![]() 踏板的长度为( )
踏板的长度为( )

A. 0.6m B. 0.65m C. 0.7m D. 0.75m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某农场要建一个长方形的养鸡场,鸡场的一边靠墙(墙长![]() 米),用木栏围成三个大小相等的长方形,木栏总长24米,总面积为32平方米.
米),用木栏围成三个大小相等的长方形,木栏总长24米,总面积为32平方米.
(1)若墙长![]() 米,求AB、BC的长.
米,求AB、BC的长.
(2)若![]() 米的墙长对鸡舍的长和宽是否有影响?请说明你的理由.
米的墙长对鸡舍的长和宽是否有影响?请说明你的理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com