
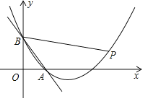
【题目】如图,直线![]() 与坐标轴交于
与坐标轴交于![]() 、
、![]() 两点,过
两点,过![]() ,
,![]() 两点的抛物线与
两点的抛物线与![]() 轴的另一交点为
轴的另一交点为![]() ,
,![]() 为抛物线上的一动点,当
为抛物线上的一动点,当![]() 时,
时,![]() 点的坐标为________.
点的坐标为________.
【答案】![]()
【解析】
先求出二次函数的解析式,然后过点B作BC⊥BP,交x轴于点C,延长BP交x轴于点D,可得∠CBA=45°,设点C坐标为(a,0),利用面积公式求出a值,然后得出点C坐标,根据BC⊥BD,BO⊥CD,可得△BCO∽DCB,进而得出![]() ,求出点D的坐标,然后求出直线BD的解析式,与二次函数解析式联立求出点P的坐标.
,求出点D的坐标,然后求出直线BD的解析式,与二次函数解析式联立求出点P的坐标.
设二次函数的解析式为y=ax2+bx+c,
则 ,
,
解得: ,
,
二次函数的解析式为:y=![]() x2-
x2-![]() x+2,
x+2,
过点B作BC⊥BP,交x轴于点C,延长BP交x轴于点D,则有∠CBA=45°,
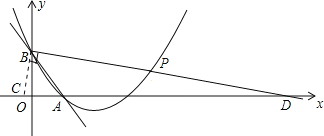
设点C坐标为(a,0)(a<0),
∵S△ABC=![]() BCABsin∠ABC=
BCABsin∠ABC=![]() ACBO,
ACBO,
∴![]() ,
,
整理得:3a2-16a-12=0,
解得:a=-![]() 或a=6(不合题意,舍去),
或a=6(不合题意,舍去),
∴点C(-![]() ,0),
,0),
∵BC⊥BD,BO⊥CD,
∴△BCO∽DCB,
则有![]() ,
,
即BC2=COCD,
∴![]() ,
,
解得:OD=6,
即点D(6,0),
∵B(0,2),
∴设直线BD的解析式为y=kx+m,
代入得:![]() ,
,
解得: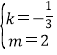 ,
,
∴直线BD的解析式为y=-![]() x+2,
x+2,
与二次函数的解析式联立得:
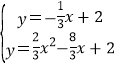 ,
,
解得:![]() ,
, ,
,
即点P的坐标为(![]() ,
,![]() ).
).
故答案为:(![]() ,
,![]() ).
).


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,爸爸和小莉在两处观测气球的仰角分别为α、β,两人的距离(BD)是100 m, 如果爸爸的眼睛离地面的距离(AB)为1.6 m,小莉的眼睛离地面的距离(CD)为1.2 m,那么气球的高度(PQ)是多少?(用含α、β的式子表示)
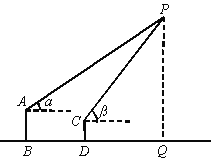
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=BC,CF交AB于E,BD⊥CF,AF⊥CF,则下列结论:①∠ACF=∠CBD②BD=FC③FC=FD+AF④AE=DC中,正确的结论是____________(填正确结论的编号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若(x2+px﹣![]() )(x2﹣3x+q)的积中不含x项与x3项
)(x2﹣3x+q)的积中不含x项与x3项
(1)求p、q的值;
(2)求代数式(﹣2p2q)2+(3pq)0+p2019q2020的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课本中有一道作业题:有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
(1)加工成的正方形零件的边长是多少mm?
(2)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少?请你计算.
(3)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.
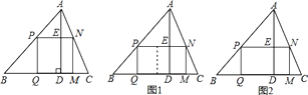
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某果园有![]() 棵枇杷树.每棵平均产量为
棵枇杷树.每棵平均产量为![]() 千克,现准备多种一些枇杷树以提高产量,但是如果多种树,那么树与树之间的距离和每一棵树接受的阳光就会减少,根据实践经验,每多种一棵树,投产后果园中所有的枇杷树平均每棵就会减少产量
千克,现准备多种一些枇杷树以提高产量,但是如果多种树,那么树与树之间的距离和每一棵树接受的阳光就会减少,根据实践经验,每多种一棵树,投产后果园中所有的枇杷树平均每棵就会减少产量![]() 千克,若设增种
千克,若设增种![]() 棵枇杷树,投产后果园枇杷的总产量为
棵枇杷树,投产后果园枇杷的总产量为![]() 千克,则
千克,则![]() 与
与![]() 之间的函数关系式为________.
之间的函数关系式为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在离旗杆6m的A处,用测角仪测得旗杆顶端C的仰角为50°,已知测角仪高AD=1.5m,求旗杆BC的高(结果是近似数,请你自己选择合适的精确度).如果你没有带计算器,也可选用如下:sin50°≈0.7660 cos50≈0.6428 tan50°≈1.192

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,在三角形纸片![]() 中,
中,![]() ,
,![]() ,将纸片的一角折叠,使点
,将纸片的一角折叠,使点![]() 落在
落在![]() 内的点
内的点![]() 处.
处.
(1)若![]() ,
,![]() ________.
________.
(2)如图①,若各个角度不确定,试猜想![]() ,
,![]() ,
,![]() 之间的数量关系,直接写出结论.
之间的数量关系,直接写出结论.
②当点![]() 落在四边形
落在四边形![]() 外部时(如图②),(1)中的猜想是否仍然成立?若成立,请说明理由,若不成立,
外部时(如图②),(1)中的猜想是否仍然成立?若成立,请说明理由,若不成立,![]() ,
,![]() ,
,![]() 之间又存在什么关系?请说明。
之间又存在什么关系?请说明。
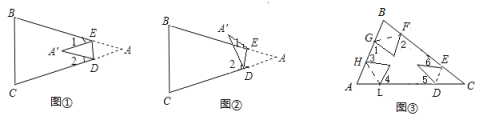
(3)应用:如图③:把一个三角形的三个角向内折叠之后,且三个顶点不重合,那么图中的![]() 和是________.
和是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com