
 已知:如图所示,直线l的解析式为y=$\frac{3}{4}$x-3,并且与x轴、y轴分别交于点A、B.
已知:如图所示,直线l的解析式为y=$\frac{3}{4}$x-3,并且与x轴、y轴分别交于点A、B.分析 (1)对于直线y=$\frac{3}{4}$x-3,令x=0,得y=-3,令y=0得,x=4,可得A、B两点坐标.
(2)设经过ts后点A在⊙P上,根据PA=1列出方程即可解决问题,注意两解.
(3))⊙P可以经过B点,理由如下:设t秒后点B在⊙P上,t秒后点P坐标(4t,0),⊙P的半径为1+6t,由题意,PB2=OB2+OP2,可得方程32+(4t)2=(1+6t)2,解方程即可.
解答 解:(1)对于直线y=$\frac{3}{4}$x-3,令x=0,得y=-3,令y=0得,x=4,
∴A(4,0),B(0,-3).
(2)设经过ts后点A在⊙P上,
∵⊙P的半径为1,
∴PA=1时,点A在⊙P上,
∴P(3,0)或(5,0),
∴4-4t=1或4t-4=1时点A在⊙P上
∴t=$\frac{3}{4}$s或$\frac{5}{4}$s时,点A在⊙P上.
(3)⊙P可以经过B点,理由如下:
设t秒后点B在⊙P上,∵t秒后点P坐标(4t,0),⊙P的半径为1+6t,
由题意,PB2=OB2+OP2,
∴32+(4t)2=(1+6t)2,
整理得5t2+3t-2=0,解得t=$\frac{2}{5}$或-1(舍弃),
∴t=$\frac{2}{5}$时,⊙P经过点B.
点评 本题考查圆综合题,点与圆位置关系,一元一次方程等知识,解题的关键是灵活运用所学知识解决问题,学会用方程的思想思考问题,属于中考常考题型.


 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=16,BC=18.连接BD,AE⊥BD,垂足为点E.
已知:如图,在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=16,BC=18.连接BD,AE⊥BD,垂足为点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
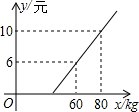 某地长途汽车客运公司规定每位旅客可随身携带一定的行李,如果超出规定,那么需要购买行李票,行李票 y(元)是行李质量 x(kg)的一次函数,其图象如图.
某地长途汽车客运公司规定每位旅客可随身携带一定的行李,如果超出规定,那么需要购买行李票,行李票 y(元)是行李质量 x(kg)的一次函数,其图象如图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com