
已知一组数据x1,x2,…,xn的方差为s2,那么另一组新数据x1+a,x2+a,…,xn+a(a≠0)的方差是
s2 .
考点: 方差.
分析: 根据方差公式进行计算,方差是用来衡量一组数据波动大小的量,每个数都加上a所以波动不会变,方差不变.
解答: 解:根据题意得:
原数据的平均数为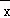 ,新数据的每一个数都加上了a,则平均数变为
,新数据的每一个数都加上了a,则平均数变为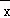 +a,
+a,
设原来的方差S2=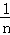 [(x1﹣
[(x1﹣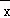 )2+(x2﹣
)2+(x2﹣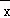 )2+…+(xn﹣
)2+…+(xn﹣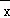 )2],
)2],
现在的方差S2=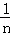 [(x1+a﹣
[(x1+a﹣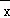 ﹣a)2+(x2+a﹣
﹣a)2+(x2+a﹣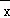 ﹣a)2+…(xn+a﹣
﹣a)2+…(xn+a﹣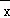 ﹣a)2]=
﹣a)2]=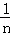 [(x1﹣
[(x1﹣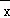 )2+(x2﹣
)2+(x2﹣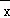 )2+…+(xn﹣
)2+…+(xn﹣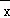 )2],
)2],
原来的方差与现在的方差一样,
则另一组新数据x1+a,x2+a,…,xn+a(a≠0)的方差是s2;
故答案为:s2.
点评: 此题考查了方差,一般地设n个数据,x1,x2,…xn的平均数为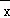 ,则方差S2=
,则方差S2=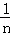 [(x1﹣
[(x1﹣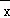 )2+(x2﹣
)2+(x2﹣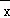 )2+…+(xn﹣
)2+…+(xn﹣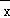 )2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.


科目:初中数学 来源: 题型:
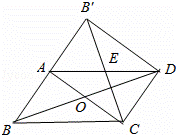
如图所示,在平行四边形ABCD纸片中,AC与BD相交于点O,将△ABC沿对角线AC翻折得到△AB′C且点B、A、B'处于同一直线上,
(1)求证:以A、C、D、B′为顶点的四边形是矩形.
(2)若四边形ABCD的面积为12cm2,求翻折后纸片重叠部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
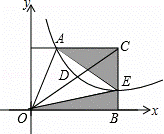
如图,在平面直角坐标系xOy中,梯形AOBC的边OB在x轴的正半轴上,AC∥OB,BC⊥OB,过点A的双曲线y=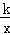 的一支在第一象限交梯形对角线OC于点D,交边BC于点E.
的一支在第一象限交梯形对角线OC于点D,交边BC于点E.
(1)填空:双曲线的另一支在第三象限,k的取值范围是k>0;
(2)若点C的坐标为(1,1),请用含有k的式子表示阴影部分的面积S.并回答:当点E在什么位置时,阴影部分面积S最小?
(3)若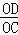 =
=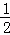 ,S△OAC=2,求双曲线的解析式.
,S△OAC=2,求双曲线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系中,将函数y=2x2的图象先向右平移1个单位,再向上平移5个单位得到图象的函数关系式是( )
A. y=2(x﹣1)2﹣5 B. y=2(x﹣1)2+5 C. y=2(x+1)2﹣5 D. y=2(x+1)2+5
查看答案和解析>>
科目:初中数学 来源: 题型:
已知函数y=mx2﹣6x+1(m是常数).
(1)求证:不论m为何值,该函数的图象都经过y轴上的一个定点;
(2)若该函数的图象与x轴只有一个交点,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
对于实数a、b,定义运算“*”:a*b=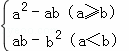 ,例如:4*2,因为4>2,所以4*2=42﹣4×2=8.若x1、x2是一元二次方程x2﹣8x+12=0的两个根,那么x1*x2=.
,例如:4*2,因为4>2,所以4*2=42﹣4×2=8.若x1、x2是一元二次方程x2﹣8x+12=0的两个根,那么x1*x2=.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com