

���� ��1�������ֱ��y=kx+k�Ľ���ʽ�������B�����꣬Ȼ���B��C����������������߽���ʽ��
��2�����������ٵ�F��ֱ��BC�Ϸ�ʱ���ڵ���F��ֱ��BC�·�ʱ���ֱ����S��FBC�����ֵ���ɴ˼��ɽ�����⣮
��3��PEƽ�֡�BPQ��QEƽ�֡�PQD�����PEQ=60�㣬���ݡ�һ�����Ƚǡ�����ģ�ͣ��ɵó���PBE�ס�EDQ���������Ʊ�����ϵ�г����̣���⼴�ɣ�
��� �⣺��1����ֱ��y=kx+k����C��-4��3����
��3=-4k+k��
��k=-1��
��y=-x-1��
��y=0����x=-1��
��B��-1��0����
��B��-1��0������-4��3�����������߽���ʽ�ã�$\left\{\begin{array}{l}{1-b+c=0}\\{16-4b+c=3}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{b=4}\\{c=3}\end{array}\right.$��
�������ߵĽ���ʽΪ��y=x2+4x+3��
��2���ٵ�F��ֱ��BC�Ϸ�ʱ����ͼ1����FD��BC��D��FE��x�ύֱ��BC��F��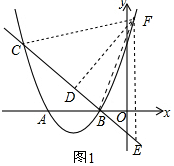
��ֱ��y=-x-1��֪��ABC=45�㣬
���DEF=45�㣬
��P��x��x2+4x+3����
��E��x��-x-1����
��EF=��x2+4x+3��-��-x-1��=x2+5x+4��
��DF=$\frac{\sqrt{2}}{2}$EF=$\frac{\sqrt{2}}{2}$��x2+5x+4����
��B��-1��0����C��-4��3����
��BC=$\sqrt{{3}^{2}+{3}^{2}}$=3 $\sqrt{2}$��
��S��FBC=$\frac{1}{2}$��3 $\sqrt{2}$��$\frac{\sqrt{2}}{2}$��x2+5x+4��=$\frac{3}{2}$��x2+5x+4����
��-3��x��$\frac{1}{2}$��
�൱x=$\frac{1}{2}$ʱ����FBC��������������=$\frac{81}{8}$��
�ڵ���F��ֱ��BC�·�ʱ����ͼ2�У���FD��BC��D��FE��x�ύֱ��BC��F��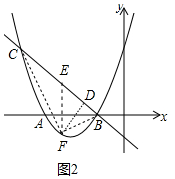
��ֱ��y=-x-1��֪��ABC=45�㣬
���DEF=45�㣬
��P��x��x2+4x+3����
��E��x��-x-1����
��EF=��-x-1��-��x2+4x+3��=-x2-5x-4��
��DF=$\frac{\sqrt{2}}{2}$EF=$\frac{\sqrt{2}}{2}$��-x2-5x-4����
��B��-1��0����C��-4��3����
��BC=$\sqrt{{3}^{2}+{3}^{2}}$=3 $\sqrt{2}$��
��S��FBC=$\frac{1}{2}$��3 $\sqrt{2}$��$\frac{\sqrt{2}}{2}$��-x2-5x-4��=-$\frac{3}{2}$��x2+5x+4��=-$\frac{3}{2}$��x+$\frac{5}{2}$��2+$\frac{27}{8}$��
��-$\frac{3}{2}$��0��
��x=-$\frac{3}{2}$ʱ����FBC�����������ֵΪ$\frac{27}{8}$��
������������FBC��������ֵΪ$\frac{81}{8}$��
��3����ͼ3��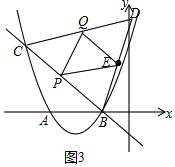
��BC=DC����BCD=60�㣬
���BCD�ǵȱ������Σ�
���CDB=��CBD=60�㣬
��PEƽ�֡�BPQ��ͬʱQEƽ�֡�PQD��
���QPE=��BPE����PQE=��DQE��
�ߡ�PEQ=90��-$\frac{1}{2}$��PCQ=90��-$\frac{1}{2}$��60��=60�㣬
�ߡ�PQE=��DQE����PEQ=��CDB=60�㣬��QPE=��BPE����PEQ=��CBD=60�㣬
���DQE�ס�EQP�ס�BEP��
��$\frac{DQ}{BE}$=$\frac{DE}{PB}$��
��BC=3 $\sqrt{2}$��CP=t��DQ=2t��
��BP=3 $\sqrt{2}$-t��
��$\frac{2t}{\frac{3\sqrt{2}}{2}}$=$\frac{\frac{3\sqrt{2}}{2}}{3\sqrt{2}-t}$��
�����ã�4t2-12 $\sqrt{2}$t+9=0��
��t=$\frac{3\sqrt{2}��3}{2}$��
�ߵ�����һ���㵽���յ�ʱ����һ������ֹ֮ͣ�˶���
��t=$\frac{3\sqrt{2}-3}{2}$��
��PB=$\frac{3\sqrt{2}+3}{2}$��
��P��$\frac{10+3\sqrt{2}}{4}$��$\frac{6+3\sqrt{2}}{4}$����
���� �����Ƕ��κ������ۺ��⣬�����˴���ϵ������һ�κ����Ͷ��κ����Ľ���ʽ�����κ�������ֵ�����������Ƶ��ж������ʣ��ȱ������ε��ж������ʣ���3��֤�á�PBE�ס�EDQ�ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
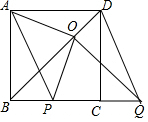 ��ͼ��BD��������ABCD�ĶԽ��ߣ�BC=2����BC�������ڵ�ֱ����ƽ�ƣ���ͨ��ƽ�Ƶõ����߶μ�ΪPQ������PA��QD��������Q��QO��BD������ΪO������OA��OP��
��ͼ��BD��������ABCD�ĶԽ��ߣ�BC=2����BC�������ڵ�ֱ����ƽ�ƣ���ͨ��ƽ�Ƶõ����߶μ�ΪPQ������PA��QD��������Q��QO��BD������ΪO������OA��OP���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ���ڡ�ABC���DCB�У�AC��BD���ڵ�E���ҡ�A=��D��AB=DC����֤��
��ͼ��ʾ���ڡ�ABC���DCB�У�AC��BD���ڵ�E���ҡ�A=��D��AB=DC����֤���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
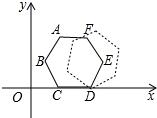 ��ͼ��ƽ��ֱ������ϵ����һ����������ABCDEF������C��D������ֱ�Ϊ��1��0���ͣ�2��0������������������£����������������x�����ҹ��������ڹ��������У���������εĶ���A��B��C��D��E��F�У�����㣨45��2�����ǣ�������
��ͼ��ƽ��ֱ������ϵ����һ����������ABCDEF������C��D������ֱ�Ϊ��1��0���ͣ�2��0������������������£����������������x�����ҹ��������ڹ��������У���������εĶ���A��B��C��D��E��F�У�����㣨45��2�����ǣ�������| A�� | ��A | B�� | ��B | C�� | ��C | D�� | ��D |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com