
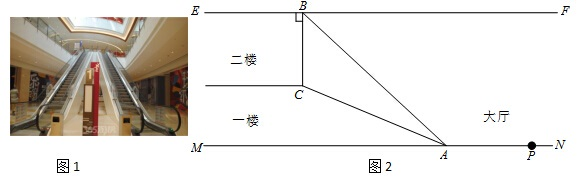
分析 (1)延长CB交MN于点H,根据坡度的定义求出HC,AH的长,然后在直角△ACH中利用三角函数即可求得BC的长;
(2)利用(1)所求得出大厅层高进而得出答案.
解答  解:(1)如图所示:延长BC交MN于H
解:(1)如图所示:延长BC交MN于H
∵BC⊥EF,EF∥MN,
∴BH⊥MN,
∵i=1:2.4=5:12=CH:AH,
∴设CH=5k,则AH=12k
在Rt△ACH中,由勾股定理AC=$\sqrt{C{H^2}+A{H^2}}$=13k,
∵AC=13m,∴k=1,
∴CH=5m,AH=12m,
设BC=x,在Rt△ACH中,tan∠BAH=$\frac{BH}{AH}$,
∴tan42°=$\frac{x+5}{12}$,
x≈5.8 m,
答:二楼层高约为5.8 m;
(2)由题得,大厅层高为BH=BC+CH=5.8+5=10.8(m),
而10+2=12m>10.8m,
∴雕像放不下.
点评 本题考查了解直角三角形的应用,用到的知识点是特殊角的三角函数值、仰角和坡度的定义,要求学生能借助仰角构造直角三角形并解直角三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
 如图,以AC为斜边在异侧作Rt△ABC和Rt△ADC,∠ABC=∠ADC=90°,∠BCD=45°,BD=4,则AC的长度为( )
如图,以AC为斜边在异侧作Rt△ABC和Rt△ADC,∠ABC=∠ADC=90°,∠BCD=45°,BD=4,则AC的长度为( )| A. | 8 | B. | 4$\sqrt{2}$ | C. | 6 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
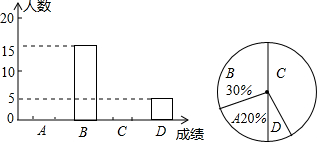 蓝天实验学校九年级一模考试后,戴主任为了解学生的学习情况,随机抽取50名学生的数学成绩(均为整数)进行统计分析,得出相关统计表和统计图如下:
蓝天实验学校九年级一模考试后,戴主任为了解学生的学习情况,随机抽取50名学生的数学成绩(均为整数)进行统计分析,得出相关统计表和统计图如下:| 成绩/分 | 111~120 | 101~110 | 91~100 | 90以下 |
| 成绩等级 | A | B | C | D |
| 人数 | m | 15 | n | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com