
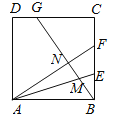
【题目】如图,正方形ABCD中,BE=EF=FC,CG=2GD,BG分别交AE,AF于M,N.下列结论:①AF⊥BG;②BN=![]() NF;③
NF;③![]() ;④
;④![]() .其中正确的结论的序号是______.
.其中正确的结论的序号是______.
【答案】①③.
【解析】
①易证△ABF≌△BCG,即可解题;
②易证△BNF∽△BCG,即可求得![]() 的值,即可解题;
的值,即可解题;
③作EH⊥AF,令AB=3,即可求得MN,BM的值,即可解题;
④连接AG,FG,根据③中结论即可求得S四边形CGNF和S四边形ANGD,即可解题.
①∵四边形ABCD为正方形,
∴AB=BC=CD,
∵BE=EF=FC,CG=2GD,
∴BF=CG,
∵在△ABF和△BCG中,
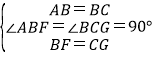 ,
,
∴△ABF≌△BCG,
∴∠BAF=∠CBG,
∵∠BAF+∠BFA=90°,
∴∠CBG+∠BFA=90°,即AF⊥BG;①正确;
②∵在△BNF和△BCG中,∠CBG=∠NBF,∠BCG=∠BNF=90°,
∴△BNF∽△BCG,
∴![]() ,
,
∴BN=![]() NF;②错误;
NF;②错误;
③作EH⊥AF,令AB=3,则BF=2,BE=EF=CF=1,
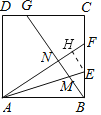
AF=![]() =
=![]() ,
,
∵S△ABF=![]() AFBN=
AFBN=![]() ABBF,
ABBF,
∴BN=![]() ,NF=
,NF=![]() BN=
BN=![]() ,
,
∴AN=AF-NF=![]() ,
,
∵E是BF中点,
∴EH是△BFN的中位线,
∴EH=![]() ,NH=
,NH=![]() ,BN∥EH,
,BN∥EH,
∴AH=![]() ,
,
![]() ,解得:MN=
,解得:MN=![]() ,
,
∴BM=BN-MN=![]() ,MG=BG-BM=
,MG=BG-BM=![]() ,
,
∴![]() ;③正确;
;③正确;
④连接AG,FG,根据③中结论,
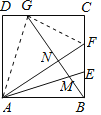
则NG=BG-BN=![]() ,
,
∵S四边形CGNF=S△CFG+S△GNF=![]() CGCF+
CGCF+![]() NFNG=1+
NFNG=1+![]() =
=![]() ,
,
S四边形ANGD=S△ANG+S△ADG=![]() ANGN+
ANGN+![]() ADDG=
ADDG=![]() ,
,
∴S四边形CGNF≠![]() S四边形ANGD,④错误.
S四边形ANGD,④错误.
故选A.


科目:初中数学 来源: 题型:
【题目】已知函数y=2mx2+(1﹣4m)x+2m﹣1,下列结论错误的是( )
A. 当m=0时,y随x的增大而增大
B. 当m=![]() 时,函数图象的顶点坐标是(
时,函数图象的顶点坐标是(![]() ,﹣
,﹣![]() )
)
C. 当m=﹣1时,若x<![]() ,则y随x的增大而减小
,则y随x的增大而减小
D. 无论m取何值,函数图象都经过同一个点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线![]() 、
、![]() 交于点
交于点![]() ,顺次联结ABCD各边中点得到的一个新的四边形,如果添加下列四个条件中的一个条件:①
,顺次联结ABCD各边中点得到的一个新的四边形,如果添加下列四个条件中的一个条件:①![]() ⊥
⊥![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,可以使这个新的四边形成为矩形,那么这样的条件个数是()
,可以使这个新的四边形成为矩形,那么这样的条件个数是()

A. 1个;B. 2个;
C. 3个;D. 4个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯运营商的手机上网流量资费标准推出了三种优惠方案:
方案A:按流量计费,0.1元/M;
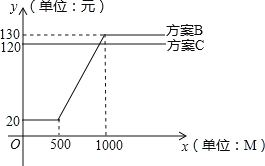
方案B:20元流量套餐包月,包含500M流量,如果超过500M,超过部分另外计费(见图象),如果用到1000M时,超过1000M的流量不再收费;
方案C:120元包月,无限制使用.
用x表示每月上网流量(单位:M),y表示每月的流量费用(单位:元),方案B和方案C对应的y关于x的函数图象如图所示,请解决以下问题:
(1)写出方案A的函数解析式,并在图中画出其图象;
(2)直接写出方案B的函数解析式;
(3)若甲乙两人每月使用流量分别在300—600M,800—1200M之间,请你分别给出甲乙二人经济合理的选择方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
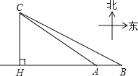
【题目】如图,在一笔直的海岸线上有![]() 、
、![]() 两个观测站,
两个观测站,![]() 在
在![]() 的正东方向,
的正东方向,![]() 千米,在某一时刻,从观测站
千米,在某一时刻,从观测站![]() 测得一艘集装箱货船位于北偏西
测得一艘集装箱货船位于北偏西![]() 的
的![]() 处,同时观测站
处,同时观测站![]() 测得改集装箱船位于北偏西
测得改集装箱船位于北偏西![]() 方向,问此时该集装箱船与海岸之间距离
方向,问此时该集装箱船与海岸之间距离![]() 约多少千米?(最后结果保留整数)
约多少千米?(最后结果保留整数)
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
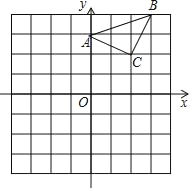
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
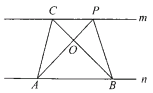
【题目】如图,直线![]() ,
,![]() 为直线
为直线![]() 上两点,
上两点,![]() 为直线
为直线![]() 上两点.
上两点.
(1)如果固定点![]() ,点
,点![]() 在直线
在直线![]() 上移动,那么不论点
上移动,那么不论点![]() 移动到何处,总有
移动到何处,总有![]() _____与
_____与![]() 的面积相等,理由是_________________.
的面积相等,理由是_________________.
(2)如果![]() 处在如图所示位置,请写出另外两对面积相等的三角形:①_________________;②_________________.
处在如图所示位置,请写出另外两对面积相等的三角形:①_________________;②_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为4,B是⊙O外一点,连接OB,且OB=6,过点B作⊙O的切线BD,切点为D,延长BO交⊙O于点A,过点A作切线BD的垂线,垂足为C.
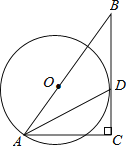
(1)求证:AD平分∠BAC;
(2)求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
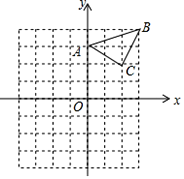
(1)△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;(画出图形)
(3)△A2B2C2的面积是 平方单位.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com