
【题目】已知,如图1,⊙O是四边形ABCD的外接圆,连接OC交对角线BD于点F,延长AO交BD于点E,OE=OF.
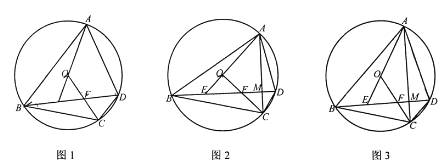
(1)求证:BE=FD;
(2)如图2,若∠EOF=90°,BE=EF,⊙O的半径![]() ,求四边形ABCD的面积;
,求四边形ABCD的面积;
(3)如图3,若AD=BC;
①求证:![]() ;②若
;②若![]() ,直接写出CD的长.
,直接写出CD的长.
【答案】(1)见详解;(2)12![]() ;(3)①见详解,②3
;(3)①见详解,②3![]() -
-![]()
【解析】
(1)如图1中,作OH⊥BD于H.根据等腰三角形的性质以及垂径定理即可;
(2)如图2中,作OH⊥BD于H,连接OB,求出AC,BD,根据S四边形ABCD=![]() BDAM+
BDAM+
![]() BDCM=
BDCM=![]() BDAC即可求解;
BDAC即可求解;
(3)①如图3中,连接OB,作OH⊥BD于H.利用等腰直角三角形的性质,完全平方公式等知识即可;
②如图3中,连接OB,设DM=CM=x,想办法求出BC,DB,在Rt△BCM中,利用勾股定理构建方程即可.
(1)证明:如图1中,作OH⊥BD于H.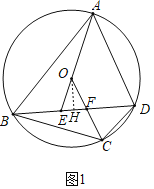
∵OE=OF,OH⊥EF,
∴EH=HF,
∵OH⊥BD,
∴BH=HD,
∴BE=DF;
(2)解:如图2中,作OH⊥BD于H,连接OB.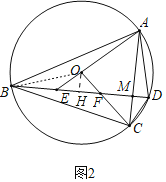
∵∠EOF=90°,OE=OF,OA=OC,
∴∠OEF=∠OAC=45°,
∴∠AME=90°,即AC⊥BD,
连接OB.设OH=a,
∵BE=EF,
∴BE=2EH=2OH=2a,
在Rt△BOH中,∵OH2+BH2=OB2,
∴a2+(3a)2=(2![]() )2,
)2,
∴a=![]() 或-
或-![]() (舍弃),
(舍弃),
∴BD=BE+EF+DF=6a=6![]() ,
,
在Rt△AOC中,AC=![]() AO=2
AO=2![]() ,
,
∴S四边形ABCD=![]() BDAM+
BDAM+![]() BDCM=
BDCM=![]() BDAC=
BDAC=![]() ×2
×2![]() ×6
×6![]() =12
=12![]() ;
;
(3)①如图3中,连接OB,作OH⊥BD于H.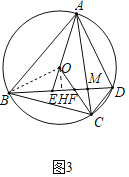
∵OE=OF,OA=OC,
∴∠EOH=![]() ∠EOF=
∠EOF=![]() (∠EAC+∠ACO)=
(∠EAC+∠ACO)=![]() ×2∠OAC=∠OAC,
×2∠OAC=∠OAC,
∴AC∥OH,
∴AC⊥BD,
∵AD=BC,
∴∠ABD=∠CAB=∠CDB=45°,
∴AB=![]() BM,CD=
BM,CD=![]() DM,CM=DM,
DM,CM=DM,
∴ABCD+BC2=![]() BM
BM![]() DM+BM2+CM2=(BM+DM)2=BD2;
DM+BM2+CM2=(BM+DM)2=BD2;
②如图3中,连接OB,设DM=CM=x,
∵∠BOC=2∠BDC=90°,
∴BC=![]() OB=2
OB=2![]() ,
,
∵ABCD+BC2=BD2,ABCD=AO2=12,
∴12+24=BD2,
∴BD=6(负根已经舍弃),
在Rt△BCM中,∵BC2=BM2+CM2,
∴(2![]() )2=(6-x)2+x2,
)2=(6-x)2+x2,
∴x=3-![]() 或3+
或3+![]() (舍弃),
(舍弃),
∴CD=![]() x=3
x=3![]() -
-![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,圆 O 的半径为 1,过点 A(2,0)的直线与圆 O 相切于点 B,与 y 轴相交于点 C.
(1)求 AB 的长;
(2)求直线 AB 的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一元二次方程![]() 满足
满足![]() ,那么我们称这个方程为“凤凰”方程.已知
,那么我们称这个方程为“凤凰”方程.已知![]() 是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是 ( )
是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC内接于⊙O,AC为⊙O的直径,点D为优弧BC的中点
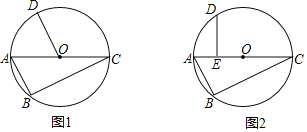
(1)如图1,连接OD,求证:AB∥OD;
(2)如图2,过点D作DE⊥AC,垂足为E.若AE=3,BC=8,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.
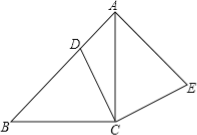
(1)求证:AB⊥AE;
(2)若BC2=ADAB,求证:四边形ADCE为正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象经过(﹣1,0)(3,0)两点,给出的下列6个结论:
①ab<0;
②方程ax2+bx+c=0的根为x1=﹣1,x2=3;
③4a+2b+c<0;
④当x>1时,y随x值的增大而增大;
⑤当y>0时,﹣1<x<3;
⑥3a+2c<0.
其中不正确的有_____.
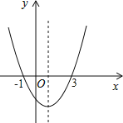
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为放置在水平桌面上的台灯的平面示意图,灯臂AO长为40cm,与水平面所形成的夹角∠OAM为75°.由光源O射出的边缘光线OC,OB与水平面所形成的夹角∠OCA,∠OBA分别为90°和30°,求该台灯照亮水平面的宽度BC(不考虑其他因素,结果精确到0.1cm.温馨提示:sin75°≈0.97,cos75°≈0.26,![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一座隧道的截面由抛物线和长方形构成,长方形的长为8m,宽为2m,隧道最高点P位于AB的中央且距地面6m,建立如图所示的坐标系:
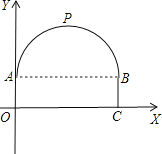
(1)求抛物线的解析式;
(2)一辆货车高4m,宽2m,能否从该隧道内通过,为什么?
(3)如果隧道内设双行道,那么这辆货车是否可以顺利通过,为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com