
【题目】重庆八中某数学兴趣小组同学探究函数 的图象与性质,根据学习函数的经验,该小组进行了系列探究.
的图象与性质,根据学习函数的经验,该小组进行了系列探究.
下表给出了自变量![]() 与函数
与函数![]() 的一些对应值:
的一些对应值:
| … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| … | 2 | 3 | 4 |
|
| 1 |
| … |
(1)补全表格:![]() ,
,![]() ;
;
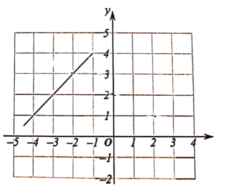
(2)在如图所示的面直角坐标系中,补全函数的图象并写出该函数的一条性质:
____________________________________________________________________________;
(3)若函数![]() ,直接写出不等式
,直接写出不等式![]() 的解集.
的解集.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小明在某次作业中得到如下结果:
sin27°+sin283°≈0.122+0.992=0.9945,
sin222°+sin268°≈0.372+0.932=1.0018,
sin229°+sin261°≈0.482+0.872=0.9873,
sin237°+sin253°≈0.602+0.802=1.0000,
sin245°+sin245°=![]() +
+![]() =1.
=1.
据此,小明猜想:对于任意锐角α,均有sin2α+sin2(90°-α)=1.
(1)当α=30°时,验证sin2α+sin2(90°-α)=1是否成立;
(2)小明的猜想是否成立?若成立,请给予证明;若不成立,请举出一个反例.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角![]() 的顶点
的顶点![]() 在正方形
在正方形![]() 的对角线
的对角线![]() 上,
上,![]() 所在的直线交
所在的直线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() . 下列结论中,正确的有_________ (填序号).
. 下列结论中,正确的有_________ (填序号).
①![]() ;②
;②![]() 是
是![]() 的一个三等分点;③
的一个三等分点;③![]() ;④
;④![]() ;⑤
;⑤![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=﹣x2+2x+3交x轴于点A、B,其中点A在点B的左边,交y轴于点C,点P为抛物线上位于x轴上方的一点.
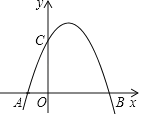
(1)求A、B、C三点的坐标;
(2)若△PAB的面积为4,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
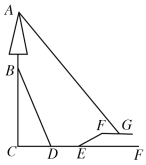
【题目】我校数学社团学生小明想测量学校对面斜坡![]() 上的信号树
上的信号树![]() 的高度,已知
的高度,已知![]() 的坡度为
的坡度为![]() ,且
,且![]() 的长度为65米,小明从坡底
的长度为65米,小明从坡底![]() 处沿直线走到学校大台阶底部
处沿直线走到学校大台阶底部![]() 处,
处,![]() 长为20米,他沿着与水平地面成
长为20米,他沿着与水平地面成![]() 夹角的大台阶行走20米到达平台
夹角的大台阶行走20米到达平台![]() 处,又向前走了13米到达平台上的旗杆
处,又向前走了13米到达平台上的旗杆![]() 处,此时他仰望信号树的顶部
处,此时他仰望信号树的顶部![]() ,测得仰角为
,测得仰角为![]() ,则信号树
,则信号树![]() 的高度约为( )(小明的身高忽略不计)
的高度约为( )(小明的身高忽略不计)
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
A.45米B.30米C.35米D.40米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等边△ABC中,D是BC的中点,P为AB 边上的一个动点,设AP=x,图1中线段DP的长为y,若表示y与x的函数关系的图象如图2所示,则△ABC的面积为( )


A. 4 B. ![]() C. 12 D.
C. 12 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径 ,点C在⊙O上,过点O作![]() 交BC于点E,交⊙O于点D,CD∥AB.
交BC于点E,交⊙O于点D,CD∥AB.
(1)求证:E为OD的中点;
(2)若CB=6,求四边形CAOD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题情境)
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.
(探究展示)
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
(拓展延伸)
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 的坐标分别为
的坐标分别为![]() 和
和![]() ,抛物线
,抛物线![]() 的顶点在线段
的顶点在线段![]() 上运动,与
上运动,与![]() 轴交于
轴交于![]() 两点(
两点(![]() 在
在![]() 的左侧),若点
的左侧),若点![]() 的横坐标的最小值为0,则点
的横坐标的最小值为0,则点![]() 的横坐标最大值为( )
的横坐标最大值为( )

A.6B.7C.8D.9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com