
 如图,已知AB是圆O的直径,AB=10,弦CD与AB相交于点N,∠ANC=30°,ON:AN=2:3,OM⊥CD,垂足为点M.
如图,已知AB是圆O的直径,AB=10,弦CD与AB相交于点N,∠ANC=30°,ON:AN=2:3,OM⊥CD,垂足为点M. 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
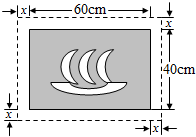 在一幅长60cm、宽40cm的矩形风景画的四周外镶一条金色纸边,制成一幅矩形挂图,如图所示.如果要使整个挂图的面积是2816cm2,那么金色纸边的宽应为多少cm?
在一幅长60cm、宽40cm的矩形风景画的四周外镶一条金色纸边,制成一幅矩形挂图,如图所示.如果要使整个挂图的面积是2816cm2,那么金色纸边的宽应为多少cm?查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| A、与x轴有两个交点,对称轴在y轴的右侧 |
| B、与x轴有两个交点,对称轴在y轴的左侧 |
| C、与x轴没有交点,对称轴在y轴的左侧 |
| D、与x轴没有交点,对称轴在y轴的右侧 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,直线y=kx-2与双曲线y=
如图,直线y=kx-2与双曲线y=| 3k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
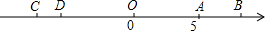 如图,数轴上有两条线段AB和CD,线段AB的长度为4个单位,线段CD的长度为2个单位,点A在数轴上表示的数是5,且A、D两点之间的距离为11.
如图,数轴上有两条线段AB和CD,线段AB的长度为4个单位,线段CD的长度为2个单位,点A在数轴上表示的数是5,且A、D两点之间的距离为11.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com