
分析 已知等式右边通分并利用同分母分式的加法法则计算,利用分式相等的条件求出A、B、C的值即可.
解答 解:已知等式整理得:$\frac{1}{(1+2x)(1+{x}^{2})}$=$\frac{A(1+{x}^{2})+(1+2x)(Bx+C)}{(1+2x)(1+{x}^{2})}$,
可得A(1+x2)+(1+2x)(Bx+C)=1,
整理得:(A+2B)x2+(B+2C)x+A+C-1=0,
可得A+2B=0,B+2C=0,A+C-1=0,
解得:A=$\frac{4}{5}$,B=-$\frac{2}{5}$,C=$\frac{1}{5}$.
点评 此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:解答题
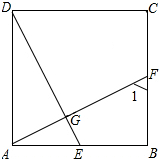
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
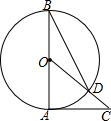 如图,AB是⊙O的直径,AC是⊙O的切线,连接OC与⊙O相交于点D,连接BD,∠C=40°,若点P为优弧$\widehat{ABD}$上的动点,连接PA、PD,则∠APD的大小是25度.
如图,AB是⊙O的直径,AC是⊙O的切线,连接OC与⊙O相交于点D,连接BD,∠C=40°,若点P为优弧$\widehat{ABD}$上的动点,连接PA、PD,则∠APD的大小是25度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
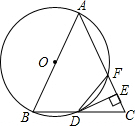 如图,以等腰△ABC的一腰AB为直径的圆交底边BC于点D,交另一腰AC于点F,连接DF,过点D作DE⊥AC于点E.
如图,以等腰△ABC的一腰AB为直径的圆交底边BC于点D,交另一腰AC于点F,连接DF,过点D作DE⊥AC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在等边△ABC中,点D在BC上,且BD=$\frac{1}{2}$CD,点E在AB上,点F在AC上,∠EDF=120°.若BE=2CF,且四边形AEDF的面积为$\frac{37\sqrt{3}}{4}$,则EF的长为$\frac{7\sqrt{15}}{5}$.
如图,在等边△ABC中,点D在BC上,且BD=$\frac{1}{2}$CD,点E在AB上,点F在AC上,∠EDF=120°.若BE=2CF,且四边形AEDF的面积为$\frac{37\sqrt{3}}{4}$,则EF的长为$\frac{7\sqrt{15}}{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com