
����Ŀ���Ķ�������ϣ� ��ͼ1����ƽ��ֱ������ϵxOy�У�ֱ��y1=ax+b��˫����y2= ![]() ����A��1��3����B����3����1�����㣮
����A��1��3����B����3����1�����㣮
�۲�ͼ���֪��
�ٵ�x=��3��1ʱ��y1=y2��
�ڵ���3��x��0��x��1ʱ��y1��y2 �� ��ͨ���۲캯����ͼ���Եõ�����ʽax+b�� ![]() �Ľ⼯��
�Ľ⼯��
������һ�����⣺��ʽx3+4x2��x��4��0�Ľ⼯��
ijͬѧ����ѧϰ����֪ʶ�ľ��飬����ʽx3+4x2��x��4��0�Ľ⼯������̽����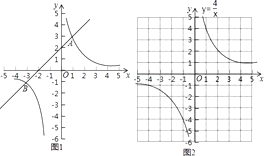
����������̽�����̣��뽫��2������3������4������������
��1���ٽ�����ʽ����������ת���� ��x=0ʱ��ԭ����ʽ��������
��x��0ʱ��ԭ����ʽ����ת��Ϊx2+4x��1�� ![]() ��
��
��x��0ʱ��ԭ����ʽ����ת��Ϊx2+4x��1�� ![]() ��
��
�ڹ��캯��������ͼ��
��y3=x2+4x��1��y4= ![]() ����ͬһ����ϵ�зֱ�������������ͼ��
����ͬһ����ϵ�зֱ�������������ͼ��
˫����y4= ![]() ��ͼ2��ʾ�����ڴ�����ϵ�л���������y3=x2+4x��1���������б���
��ͼ2��ʾ�����ڴ�����ϵ�л���������y3=x2+4x��1���������б���
��2��ȷ����������ͼ����ĺ����� �۲���������������ͼ���벢ͨ�����뺯������ʽ��֤��֪������y3=y4������x��ֵΪ
��3������ͼ��д���⼯ ��ϣ�1�������۽�����۲�����������ͼ���֪������ʽx3+4x2��x��4��0�Ľ⼯Ϊ ��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC �У���A+��B =900.
�Ÿ���Ҫ��ͼ��
�ٹ���C��ֱ�� MN ��AB
�ڹ���C��AB�Ĵ��ߣ���AB�ڵ�D.
�����ڢŵĻ����ϻش��������⣺
����֪��B+��DCB=900�����A���DCB �Ĵ�С��ϵΪ__________��������__________.
��ͼ���߶�_________�ij��ȱ�ʾ�� A ��ֱ��CD�ľ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������A��O��B��ʾ�����ֱ�Ϊ6��0����4������P��A��������ÿ��6����λ���ٶ����������������˶�.
��1������P����A�ľ������P����B�ľ������ʱ����P�������ϱ�ʾ������ ��
��2����һ����R��B��������ÿ��4����λ���ٶ����������������˶�������P��Rͬʱ�������ʵ�P�˶�����ʱ���ϵ�R��
��3����MΪAP���е㣬NΪPB���е㣬��P���˶������У��߶�MN�ij����Ƿ����仯���������仯������˵�����ɣ������䣬���㻭��ͼ�Σ�������߶�MN�ij���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������й���ͳ��ѧ��Ҫ���������춨���й���ͳ��ѧ�Ļ�����ܣ��������������м��أ�������Բ�ģ����ڱ��У���֪��С���Ծ��֮����һ�磬�����һ�ߣ��侶���Σ�������ͼ�٣� 
�Ķ���������ֺ�С�ǻ�����һ��Բ������ʾ��ͼ����ͼ�ڣ�������BO��CD�ڵ�A����侶����Ҫ���O��ֱ����
��1���ٴ��Ķ�����AB=�磬CD=�磨һ�ߵ���ʮ�磩��ͨ�������й�֪ʶ���ɽ��������⣮���㲹ȫ��Ŀ������
��2������С�������O��ֱ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������y=x2+��2m��1��x+m2��1��������ԭ�㣬�ҵ�x��0ʱ��y��x���������С��
��1���������ߵĽ���ʽ��
��2�����ͼ��д����0��x��4ʱ��ֱ��д��y��ȡֵ��Χ��
��3�����A�Ǹ���������λ��x���·���һ�����㣬����A��x���ƽ���߽�����������һ��D������AB��x���ڵ�B��DC��x���ڵ�C����BC=1ʱ���������ABCD���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����֪��|a|=3��b2=4��ab��0����a��b��ֵ��
��2����֪����x�ķ���![]() =
=![]() �뷽��
�뷽��![]() =3y��2�Ľ⻥Ϊ��������m��ֵ��
=3y��2�Ľ⻥Ϊ��������m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AOB��ֱ�ǣ�OAƽ�֡�COD��OEƽ�֡�BOD������BOE=23�������BOC�Ķ����ǣ�������
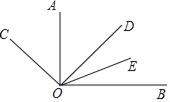
A. 113�� B. 134�� C. 136�� D. 144��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��OC�ڡ�BOD�ڣ�
��1�������AOC�͡�BOD����ֱ�ǣ�
������BOC=60�������AOD�Ķ������� ����
�ڲ����BOC���AOD��������ϵ����˵�����ɣ�
��2�������AOC=��BOD=x������AOD=y�������BOC�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB��x�ύ�ڵ�A��1��0������y�ύ�ڵ�B��0����2���� 
��1����ֱ��AB�Ľ���ʽ��
��2����ֱ��AB�ϵĵ�C�ڵ�һ���ޣ���S��BOC=2������C�ķ����������Ľ���ʽ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com